運算元分裂法(method of splitting operators)是指一類偏微分方程數值解法,指把複雜的運算元分裂成幾個較簡單的子運算元之積而導出的數值解法,它既適用於典型的雙曲型方程和拋物型方程,也適用於更複雜方程的初邊值問題之求解。
基本介紹
- 中文名:運算元分裂法
- 外文名:method of splitting operators
- 性質:一類偏微分方程數值解法
- 相關概念:偏微分方程、數值解法等
基本介紹
意義
基本原理
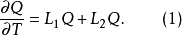
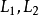
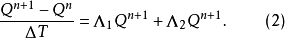
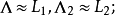
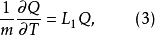
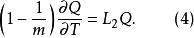
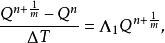
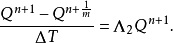

運算元分裂法(method of splitting operators)是指一類偏微分方程數值解法,指把複雜的運算元分裂成幾個較簡單的子運算元之積而導出的數值解法,它既適用於典型的雙曲型方程和拋物型方程,也適用於更複雜方程的初邊值問題之求解。
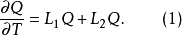
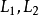
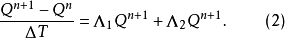
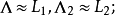
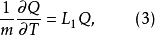
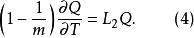
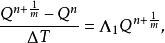
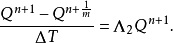
運算元分裂法(method of splitting operators)是指一類偏微分方程數值解法,指把複雜的運算元分裂成幾個較簡單的子運算元之積而導出的數值解法,它既適用於典型的雙曲型...
143、張志輝、薛禹群、謝春紅、吳吉春,1994,運算元分裂法在對流占優三維對流-彌散問題中的套用,計算物理,Vol.11,No.1,pp38-44。 144、 薛禹群、謝春紅、張志輝、...
80年代初期,他又引入運算元分裂法的思路指導學生開發破開運算元法計算程式,進一步縮短了計算機時,獲得了具有工程上可接受的良好精度。林秉南1958年受命進行研究水庫潰壩洪水...
基於有限元程式自動生成系統(FEPG),將運算元分裂法和最小二乘法相結合,求解了N-S方程,進行了粘性不可壓流體的繞圓柱流的研究。進行了湍流模型的研究,通過混合插值...
例如,大慶油田在三維空間格線化技術、熱史模型等方面都有所進展;勝利油田與山東大學合作,採用運算元分裂法求解三維模型,推出視三維盆地模擬系統(SL3DBS);西北石油地質...
全書共分6章, 內容包括預備知識、圖像反問題病態性數值分析及正則化方法、自適應正則化參數估計和基於運算元分裂的圖像反問題並行求解方法等。...
1.3.1水頭方程的運算元分裂法 1.3.2鹽分濃度方程的迎風加權分裂算法 1.3.3數值模擬過程及框圖 參考文獻 第2章數值模擬結果比較和數值分析 2.1數值模擬...
歐拉描述的運動描述方法、守恆方程及其有限元離散格式(含彼得羅夫-伽遼金有限元)和格線更新算法,並講述了求解歐拉法和任意拉格朗日-歐拉法控制方程的運算元分裂法和輸運...
4.3.3運算元分裂方法4.3.4非交錯格線下壓力——速度耦合方程4.3.5差分方程組求解4.4macconnack算法4.5邊界條件4.5.1人口邊界條件4.5.2出口邊界條件...
《非線性隨機動力學的若干數值方法及套用》詳細介紹胞映射方法、路徑積分方法、自由格線路徑積分和運算元分裂方法及它們的套用,以及正交多項式逼近方法及其在隨機結構動力...
《偏微分方程現代數值方法(科學版)》內容包括微分方程變分原理及其逼近,有限元方法,有限元誤差估計及其套用,有限體積法和譜方法,分裂算法(包括區域和運算元兩類),多...
2.10 解隱格式方程的疊代法和追趕法 2.11 多步顯格式 2.12 多維問題的運算元分裂法 2.13 交錯方向法(ADI法) 2.14 非線性對流擴散方程的交錯方向法 ...
8.1.4Strang運算元分裂法 8.1.5非定常流的雙時間步長法 8.1.6化學反應源項的處理 8.1.7控制方程的空間離散 8.1.8控制方程的時間離散 8.2計算模...
在河道等水位線圖上,將計算域縱設167格線、橫設33格線,對上面方程組採用運算元分裂法差分運算,預測175米設計水位下,入庫保證率為90%最枯月平均流量、連續7天最枯...
