進制轉換

進制轉換是人們利用符號來計數的方法。進制轉換由一組數碼符號和兩個基本因素“基數”與“位權”構成。

基數是指，進位計數制中所採用的數碼（數制中用來表示“量”的符號）的個數。

位權是指，進位制中每一固定位置對應的單位值。

基本介紹

• 中文名：進制轉換
• 基本因素：基數和位權
• 基本解釋：人們利用符號來計數的方法
• 基數：進位計數制中所採用的數碼的個數

進制轉換本質

我們知道十進制轉換成二進制用短除法，但是為什麼用短除法呢？請往下看。

“數制”只是一套符號系統來表示指稱“量”的多少。我們用“1”這個符號來表示一個這一“量”的概念。自然界的“量”是無窮的，我們不可能為每一個“量”都造一個符號，這樣的系統沒人記得住。所以必須用有限的符號按一定的規律進行排列組合來表示這無限的“量”。符號是有限的，這些符號按照某種規則進行排列組合的個數是無限的。十進制是10個符號的排列組合，二進制是2個符號的排列組合。

在進行進制轉換時有一基本原則：轉換後表達的“量”的多少不能發生改變。二進制中的111個蘋果和十進制中的7個蘋果是一樣多的。

十進制中的數位排列是這樣的…… 萬 千 百 十 個 十分 百分 千分……

R進制中的數位排列是這樣的……R^4 R^3R^2 R^1 R^0 R^-1 R^-2 R^-3……

可以看出相鄰的數位間相差進制的一次方。

以下部分來源：知乎網友

進制這事兒，說到底就是位值原理，即：同一個數字，放在不同的數位上，代表不同大小的“量”。例如：十進制中，百位上的1表示100，十位上的1表示10。

任何進制中，每個數都可以按位權展開成各個數位上的數字乘以對應數位的位權，再相加的形式，如：
十進制的123=1×100+2×10+3×1
十進制的9876=9×1000+8×100+7×10+6×1
問：為啥相應的數位是1000、100、10、1？為啥不是4、3、2、1？

答：十進制，滿十進一，再滿十再進一，因此要想進到第三位，得有10×10；第4位得有10×10×10

這樣我們就知道了：

對10進制，從低位到高位，依次要乘以10^0，10^1,10^2,10^3……，也就是1、10、100、1000
對2進制，從低位到高位，依次要乘以2^0，2^1,2^2,2^3……，也就是1、2、4、8、……
下面我們開始轉換進制（以十進制換成二進制為例）：
原來十進制咱們的數位叫 千位、百位、十位……
現在二進制數位變成了八位、四位、二位……
模仿上面十進制按位權展開的方式，把二進制數1011按權展開： 1011=1×2^3+0×2^2+1×2^1+1×2^0=1×8+0×4+1×2+1×1=8+2+1=11
接下來我們進行十進制往二進制的轉換：
比較小的數，直接通過拆分就可以轉換回去
比如13，我們把數位擺好八位、四位、二位，不能寫十六了，因為一旦“十六”那個數位上的符號是“1”，那就表示有1個16，即便後面數位上的符號全部是“0”，把這個二進制數按權位展開後，在按照十進制的運算規律計算，得到的數也大於13了。那最多就只能包含“八”這個數位。 13-8=5，5當中有4，5-4=1
好啦，我們知道13=1*8+1*4+0*2+1*1 把“1”、“1”、“0”“1”這幾個符號放到數位上去：

八位、四位、二位、一位
1 1 0 1
於是十進制數13=二進制數1101
現在你按照書上說的短除法來試試，會發現它和你湊數得到的結果剛好是一樣的，為什麼短除法可以實現進制的轉換呢？為什麼每次要除以進制呢？為什麼要把餘數倒著排列呢？
想要知道其中的道理的話，請仔細品味以下的遞歸原理（不知道遞歸沒關係）：
（1）一個十進制數321的末尾是1，意味著一定是……+1，省略號部分一定是10的倍數，所以一個十進制數末尾是1意味著十進制數除以進制10一定餘1。所以第一次除以10之後的餘數，應該放在十進制的最後一個數位“個位”，也就是說個位上的符號是1。

類比，一個二進制數111（注意，數值不等於上面十進制的111）末尾是1，意味著一定是……+1，前面的省略號部分都是2的倍數。所以一個二進制數末尾是1，意味著它對應的十進制數除以進制2一定餘1。所以第一次除以2之後的餘數，應該放在二進制的最後一個數位“一位”，也就是說一位上的符號是1。

（2）如果一個十進制數321“十位”是2，我們希望把它轉換為（1）的情況。那么我們把這個十進制數的末尾抹掉，也就是減去“個位”上的1，再除以進制10，得到32。這樣原來“十位”上的“2”就掉到了“個位”上。再把32做（1）的處理。

類比，如果一個二進制數111“二位”是1，我們希望把它轉換為（1）的情況，那么我們把這個二進制數的末尾抹掉，也就是減去“一位”上的1，再除以進制2，得到11。這樣原來“二位”上的“1”就掉到了“一位”上。再把11做（1）的處理。

總結：其實這個過程就是把各個數位上的符號求出來的過程。

現在你應該可以回答以下問題了：為什麼短除法可以實現進制的轉換呢？為什麼每次要除以進制呢？為什麼要把餘數倒著排列呢？

R進制轉換成十進制就是按權位展開，把展開式放到十進制下，再按照“十進制”的運算規律計算。因為是十進制，所以就允許使用2、3、4、5、6、7、8、9了。所以2的n次方就不用寫成指數，而可以用另外的八個符號來表示了。

十進制--->二進制

對於整數部分，用被除數反覆除以2，除第一次外，每次除以2均取前一次商的整數部分作被除數並依次記下每次的餘數。另外，所得到的商的最後一位餘數是所求二進制數的最高位。

對於小數部分，採用連續乘以基數2，並依次取出的整數部分，直至結果的小數部分為0為止。故該法稱“乘基取整法”。

給你一個十進制，比如：6，如果將它轉換成二進制數呢？

10進制數轉換成二進制數，這是一個連續除以2的過程：

把要轉換的數，除以2，得到商和餘數，

將商繼續除以2，直到商為0。最後將所有餘數倒序排列，得到數就是轉換結果。

聽起來有些糊塗？結合例子來說明。比如要轉換6為二進制數。

“把要轉換的數，除以2，得到商和餘數”。

那么：要轉換的數是6， 6 ÷ 2，得到商是3，餘數是0。

十轉二示意圖

“將商繼續除以2,直到商為0……”

現在商是3，還不是0，所以繼續除以2。

那就： 3 ÷ 2, 得到商是1,餘數是1。

“將商繼續除以2，直到商為0……”

現在商是1，還不是0，所以繼續除以2。

那就： 1 ÷ 2, 得到商是0，餘數是1

“將商繼續除以2，直到商為0……最後將所有餘數倒序排列”

好極！現在商已經是0。

我們三次計算依次得到餘數分別是：0、1、1，將所有餘數倒序排列，那就是：110了！

6轉換成二進制，結果是110。

把上面的一段改成用表格來表示，則為：

被除數	計算過程	商	餘數
6	6/2	3	0
3	3/2	1	1
1	1/2	0	1

（在計算機中，÷用 / 來表示）

二進制--->十進制

二進制數轉換為十進制數

二進制數第0位的權值是2的0次方，第1位的權值是2的1次方……

所以，設有一個二進制數：0110 0100，轉換為10進制為：

下面是豎式：

0110 0100 換算成十進制

第0位 0 * 2⁰ = 0

第1位 0 * 2¹ = 0

第2位 1 * 2² = 4

第3位 0 * 2³ = 0

第4位 0 * 2⁴ = 0

第5位 1 * 2⁵ = 32

第6位 1 * 2⁶ = 64

第7位 0 * 2⁷ = 0

公式：第N位2^(N)

---------------------------

100

用橫式計算為：

0 * 2⁰ + 0 * 2¹ + 1 * 2² + 0 * 2³ + 0 * 2⁴ + 1 * 2⁵ + 1* 2⁶ + 0 * 2⁷ = 100

0乘以多少都是0，所以我們也可以直接跳過值為0的位：

1 * 2² + 1 * 2⁵ +1*2⁶ = 100

十進制--->八進制

10進制數轉換成8進制的方法，和轉換為2進制的方法類似，唯一變化：除數由2變成8。

來看一個例子，如何將十進制數120轉換成八進制數。

用表格表示：

被除數	計算過程	商	餘數
120	120/8	15	0
15	15/8	1	7
1	1/8	0	1

120轉換為8進制，結果為：170。

八進制--->十進制

八進制就是逢8進1。

八進制數採用 0～7這八數來表達一個數。

八進制數第0位的權值為8的0次方，第1位權值為8的1次方，第2位權值為8的2次方……

所以，設有一個八進制數：1507，轉換為十進制為：

用豎式表示：

1507換算成十進制。

第0位 7 * 8⁰ = 7

第1位 0 * 8¹ = 0

第2位 5 * 8² = 320

第3位 1 * 8³ = 512

--------------------------

839

同樣，我們也可以用橫式直接計算：

7 * 8⁰ + 0 * 8¹ + 5 * 8² + 1 * 8³ = 839

結果是，八進制數 1507 轉換成十進制數為 839

十進制--->十六進制

10進制數轉換成16進制的方法，和轉換為2進制的方法類似，唯一變化：除數由2變成16。

同樣是120，轉換成16進制則為：

被除數	計算過程	商	餘數
120	120/16	7	8
7	7/16	0	7

120轉換為16進制，結果為：78。

十六進制--->十進制

16進制就是逢16進1，但我們只有0~9這十個數字，所以我們用A，B，C，D，E，F這六個字母來分別表示10，11，12，13，14，15。字母不區分大小寫。

十六進制數的第0位的權值為16的0次方，第1位的權值為16的1次方，第2位的權值為16的2次方……

所以，在第N（N從0開始）位上，如果是是數 X （X 大於等於0，並且X小於等於 15，即：F）表示的大小為 X * 16的N次方。

假設有一個十六進數 2AF5, 那么如何換算成10進制呢？

用豎式計算：

2AF5換算成10進制:

第0位： 5 * 16⁰ = 5

第1位： F * 16¹ = 240

第2位： A * 16² = 2560

第3位： 2 * 16³ = 8192

-------------------------------------

10997

直接計算就是：

5 * 16⁰ + F * 16¹ + A * 16² + 2 * 16³ = 10997

(別忘了，在上面的計算中，A表示10，而F表示15)

現在可以看出，所有進制換算成10進制，關鍵在於各自的權值不同。

假設有人問你，十進數 1234 為什麼是 一千二百三十四？你盡可以給他這么一個算式：

1234 = 1 * 10³ + 2 * 10² + 3 * 10¹ + 4 * 10⁰

二進制--->八進制

（11001.101）（二）

整數部分：從後往前每三位一組，缺位處用0填補，然後按十進制方法進行轉化， 則有：

001=1

011=3

然後我們將結果按從下往上的順序書寫就是：31，那么這個31就是二進制11001的八進制形式

八進制--->二進制

（31.5）（八）

整數部分：從後往前每一位按十進制轉化方式轉化為三位二進制數，缺位處用0補充 則有：

1---->1---->001

3---->11

然後我們將結果按從下往上的順序書寫就是：11001，那么這個11001就是八進制31的二進制形式

二進制--->十六進制

二進制和十六進制的互相轉換比較重要。不過這二者的轉換卻不用計算，每個C，C++程式設計師都能做到看見二進制數，直接就能轉換為十六進制數，反之亦然。

我們也一樣，只要學完這一小節，就能做到。

首先我們來看一個二進制數：1111，它是多少呢？

你可能還要這樣計算：1 * 2⁰ + 1 * 2¹ + 1 * 2² + 1 * 2³ = 1 * 1 + 1 * 2 + 1 * 4 + 1 * 8 = 15。

然而，由於1111才4位，所以我們必須直接記住它每一位的權值，並且是從高位往低位記，：8、4、2、1。即，最高位的權值為2³ = 8，然後依次是 2² = 4，2¹=2， 2⁰ = 1。

記住8421，對於任意一個4位的二進制數，我們都可以很快算出它對應的10進制值。

下面列出四位二進制數xxxx 所有可能的值（中間略過部分）

僅四位的二進制數	快速計算方法	十進制值	十六進制值
1111	8+4+2+1	15	F
1110	8+4+2+0	14	E
1101	8+4+0+1	13	D
1100	8+4+0+0	12	C
1011	8+0+2+1	11	B
1010	8+0+2+0	10	A
1001	8+0+0+1	9	9
……
0001	0+0+0+1	1	1
0000	0+0+0+0	0	0

二進制數要轉換為十六進制，就是以4位一段，分別轉換為十六進制。

如：

二進制數	1111 1101	1010 0101	1001 1011
對應的十六進制數	FD	A5	9B

十六進制--->二進制

反過來，當我們看到 FD時，如何迅速將它轉換為二進制數呢？

先轉換F：

看到F，我們需知道它是15（可能你還不熟悉A～F這六個數），然後15如何用8421湊呢？應該是8 + 4 + 2 + 1，所以四位全為1 ：1111。

接著轉換 D：

看到D，知道它是13，13如何用8421湊呢？應該是：8 + 4 + 1,即：1101。

所以,FD轉換為二進制數，為： 1111 1101

由於十六進制轉換成二進制相當直接，所以，我們需要將一個十進制數轉換成2進制數時，也可以先轉換成16進制，然後再轉換成2進制。

比如，十進制數 1234轉換成二制數，如果要一直除以2，直接得到2進制數，需要計算較多次數。所以我們可以先除以16，得到16進制數:

被除數	計算過程	商	餘數
1234	1234/16	77	2
77	77/16	4	13(D)
4	4/16	0	4

結果16進制為： 0x4D2

然後我們可直接寫出0x4D2的二進制形式： 0100 1101 0010。

其中對映關係為：

0100 -- 4

1101 -- D

0010 -- 2

同樣，如果一個二進制數很長，我們需要將它轉換成10進制數時，除了前面學過的方法是，我們還可以先將這個二進制轉換成16進制，然後再轉換為10進制。

下面舉例一個int類型的二進制數：

01101101 11100101 10101111 00011011

我們按四位一組轉換為16進制： 6D E5 AF 1B

再轉換為10進制：6*16⁷+D*16⁶+E*16⁵+5*16⁴+A*16³+F*16²+1*16¹+B*16⁰=1,843,769,115

十進制--->負進制

下面是將十進制數轉換為負R進制的公式：

N=(dmdm-1...d1d0)-R

=dm*_(-R)^m+dm-1*_(-R)^m-1+...+d1*_(-R)¹+d0*(-R)⁰

15=1*_(-2)⁴+0*_(-2)³+0*_(-2)²+1*_(-2)¹+1*_(-2)⁰

=10011_(-2)

負數

負數的進制轉換稍微有些不同。

先把負數寫為其補碼形式（在此不議），然後再根據二進制轉換其它進制的方法進行。

例：要求把-9轉換為八進制形式。則有：

-9的補碼為1111 1111 1111 0111。從後往前三位一划，不足三位的加0

111---->7

110---->6

111---->7

111---->7

111---->7

001---->1

然後我們將結果按從下往上的順序書寫就是：177767，那么177767就是十進制數-9的八進制形式。

其實轉化成任意進制都是一樣的。

初學者最容易犯的錯誤！！！！！！！

犯錯：（-617）D=（-1151）O=（-269）H

原因分析：如果是正數的話，上面的思路是正確的，但是由於正數和負數在原碼、反碼、補碼轉換上的差別，所以按照正數的求解思路去對負數進行求解是不對的。

正確的方法是：首先將-617用補碼錶示出來，然後再轉換成八進制和十六進制（補碼）即可。

註：二進制補碼要用16位。

正確答案：：（-617）D=（176627）O=（fd97）H

負數十進制轉換成八進制或十六進制方法

如（-12）10=（　）8=（　）16

第一步：轉換成二進制

1000 0000 0000 1100

第二步：補碼，取反加一

注意：取反時符號位不變！

1111 1111 1111 0100

第三步：轉換成八進制是三位一結合：177764（8）

轉換成十六進制是四位一結合：fff4（16）

小數

最近有些朋友提了這樣的問題“0.8的十六進制是多少？”

0.8、0.6、0.2... ...一些數字在進制之間的轉化過程中確實存在麻煩。

就比如“0.8的十六進制”吧！

無論怎么乘以16，它的餘數總也乘不盡，總是餘0.8

具體方法如下：

0.8*16=12.8

0.8*16=12.8

取每一個結果的整數部分為12既十六進制的C

如果題中要求精確到小數點後3位那結果就是0.CCC

如果題中要求精確到小數點後4位那結果就是0.CCCC

現在OK了。

C++

十進制轉k進制

#include<cstdio>#include<iostream>#include<ctime>char a[1000];using namespace std;int main(){    int y=0,k,n,x;    char z='A';    scanf ("%d %d",&n,&x);    while (n!=0)    {             y++;             a[y]=n%x;          n=n/x;          if (a[y]>9) a[y]=z+(a[y]-10);           else a[y]=a[y]+'0';    }    for (int i=y;i>0;i--)    printf ("%c",a[i]);    return 0;}

m進制轉10進制

#include<cstdio>#include<iostream>#include<cstdlib>#include<cstring>char a[10000];using namespace std;int main(){   int n,m;   int f=0;   scanf ("%s%d",a,&m);   for (int i=0;i<strlen(a);i++)   {        f*=m;        if (a[i]=='A'||a[i]=='B'||a[i]=='C'||a[i]=='D'||a[i]=='E'||a[i]=='F')        {            f=f+(a[i]-'A'+10);        }        else        {            f=f+(a[i]-'0');        }   }   printf ("%d",f);   return 0;}

註：用C語言的格式化輸入輸出可以快速轉換10進制，8進制和16進制。例子：10進制轉16進制：

#include <cstido>int main(){    int a;    scanf("%d",&a);    printf("%x",a);    return 0;}

C語言代碼

#include<stdio.h>#include<math.h>intmain(){longn,m,r;while(scanf("%ld%ld",&n,&r)!=EOF){if(abs(r)>1&&!(n<0&&r>0)){longresult[100];long*p=result;printf("%ld=",n);if(n!=0){while(n!=0){m=n/r;*p=n-m*r;if(*p<0&&r<0){*p=*p+abs(r);m++;}p++;n=m;}for(m=p-result-1;m>=0;m--){if(result[m]>9)printf("%c",55+result[m]);elseprintf("%d",result[m]);}}elseprintf("0");printf("(base%d)\n",r);}}return0;}

/*以下為10進制以下轉換。。。*//*用函式，可直接拷貝。。。*//*(VS2008環境下C++控制台代碼)*/#include"stdafx.h"#include<stdio.h>intx[100];intjzzh(inty,intml){inti,j;i=ml;x[0]=0;for(inta=1;;a++){if(i!=0){x[a]=i%y;x[0]++;}elsebreak;i=i/y;}returnx[0];}

intmain(intargc,char*argv[]){printf("Hello,world\n");longinty,ml;longinta;printf("請輸入需要轉換至進制數：");scanf("%d",&y);printf("請輸入數字：");scanf("%d",&ml);jzzh(y,ml);for(a=x[0];a>=1;a--)printf("%d",x[a]);printf("\n");return0;}

Java代碼

Java代碼實現十進制分別轉換為十六，二，八進制。

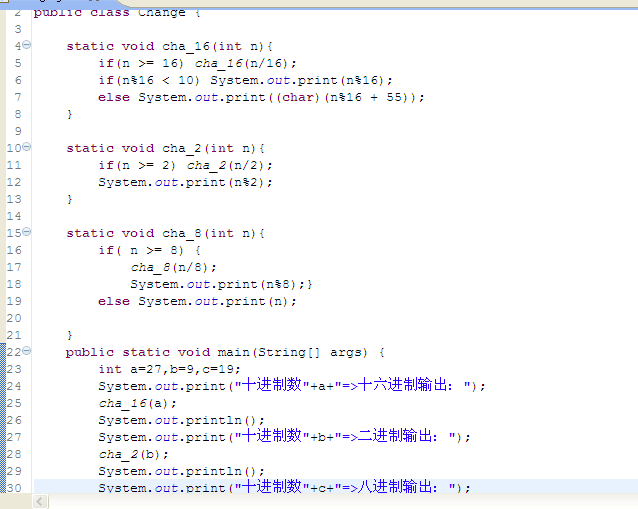Java代碼

核心思想就是餘數定理。

public class Change { /*轉為16進制*/ static void cha_16(int n)

{ if(n >= 16) cha_16(n/16);

if(n%16 < 10)System.out.print(n%16);

else System.out.print((char)(n%16 + 55)); } /*轉為2進制*/

static void cha_2(int n)

{ if(n >= 2) cha_2(n/2);

System.out.print(n%2); } /*轉為8進制*/

static void cha_8(int n)

{ if( n >= 8) { cha_8(n/8);

System.out.print(n%8); }

else System.out.print(n); } /*主程式入口*/

public static void main(String[] args)

{ int a=27,b=9,c=19; /*定義輸入的轉換數值*/ System.out.print("十進制數"+a+"=>十六進制輸出：");

cha_16(a); System.out.println(); /*換行*/

System.out.print("十進制數"+b+"=>二進制輸出：");

cha_2(b); System.out.println();

System.out.print("十進制數"+c+"=>八進制輸出：");

cha_8(c); }}