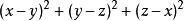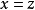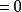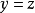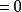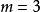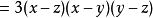餘數定理

餘數定理（Polynomial remainder theorem）是指一個多項式f(x) 除以一個線性多項式(x-a)的餘數是 f(a)。若f(a)=0，則(x-a)為多項式f(x)的因式。例如，(5x³+4x²-12x+1)/(x-3) 的餘式是 5·3³+4·3²-12·3+1=136。

基本介紹

• 中文名：餘數定理
• 外文名：Remainder Theorem
• 學科：數學
• 屬性：定理
• 定理內容：多項式f(x)除以x-a的餘數是f(a)
• 用於：求餘數；因式分解

餘數定理

多項式f(x)除以(x-a)所得的餘數等於f(a)。

推論：

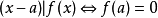
證明

根據除法的定義及性質可知，被除數=除數×商+餘數。

設多項式 除以一次式 所得的商為 ，餘數為 ，根據上面的性質可以列出下列恆等式：

令 ，代入上式即得 ，因此得到結論： 除以 後的餘數 。

注意：若除式不為 的類型，依然可以利用上面的方法來求餘數（式），即先求出使除式為0的x的值，再代入恆等號兩邊。

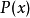
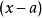
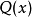
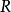
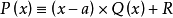
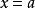
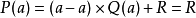
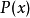
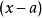
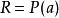
推廣形式

設 是 n 個不同的數，而 ，對任意多項式 用除所得 的餘式為

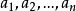
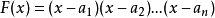
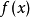
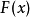
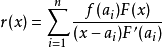
例題

一次項係數不為1

例：求 的餘數。

解：在這裡 ，使除式為 的 ，所以餘數為 。

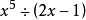
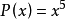
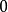
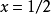
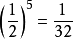
除式次數大於1

例1：求 的餘式。

解：由於除式是2次多項式，所以設餘式為 （餘式的次數要比除式低1）。

的解為 或，代入恆等式 的兩邊得：

解得 。

故餘式為

例2：求 的餘式。

解：除式的次數為3，所以設餘式為 。由於的解為或 ，代入恆等式得：

出現等式個數少於待定係數的個數時需要把恆等式兩邊對x求導，再把解代入求導後的等式中。

對 左右兩邊求導得

再把代入，得到第三個等式：

解方程組得

所以餘式為

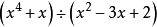
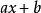
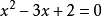
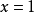
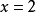
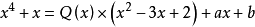
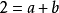
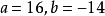
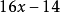
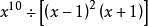
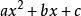
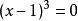
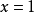
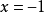
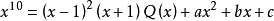
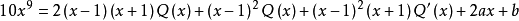
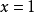
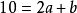
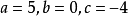
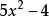
因式分解

因式分解

解：易知當時，原式。當 與 時亦有原式

∴將多項式展開後應含有因式

設原式，則展開後比較係數可得：

∴原式