廣義剩餘定理

廣義剩餘定理亦稱廣義貝祖定理，是餘數定理在矩陣多項式上的推廣。

基本介紹

• 中文名：廣義剩餘定理
• 外文名：generalized remainder theorem
• 適用範圍：數理科學

簡介

廣義剩餘定理亦稱廣義貝祖定理，是餘數定理在矩陣多項式上的推廣。

給定數域P上的矩陣多項式

其中F₀，F₁，...，F_m為P上的n階矩陣，且F₀≠0，則以λE-A右除F(λ)所得的餘式為

以λE-A左除F(λ)所得的餘式為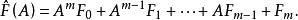

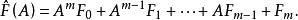
λE-A右（左）整除矩陣多項式F(λ)的充分必要條件是：。

餘數定理

（Polynomial remainder theorem）

餘數定理是指一個多項式f(x) 除以一個線性多項式(x-a)的餘數是 f(a)。若f(a)=0，則(x-a)為多項式f(x)的因式。例如，(5x³+4x²-12x+1)/(x-3) 的餘式是 5·3³+4·3²-12·3+1=136。

矩陣多項式

(matrical polynomial)

矩陣多項式是一種特殊矩陣。設A₀，A₁，…，A_s是數域P上的m×n矩陣，λ是一個文字，則A₀λ_s+A₁λ_s-1+…+A_s-1λ+A_s稱為矩陣多項式。

矩陣多項式涉及有矩陣多項式的運算、矩陣多項式的右（左）除。