連續系統數字仿真方法是指用數字計算機對連續系統進行仿真的方法。採用這種方法時首先將連續系統的數學模型轉變為適合在數字計算機上進行試驗的仿真模型,實現這種轉變的計算方法主要有微分方程數值解法和離散相似法。
微分方程數值解法
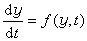
連續系統數字仿真方法是指用數字計算機對連續系統進行仿真的方法。採用這種方法時首先將連續系統的數學模型轉變為適合在數字計算機上進行試驗的仿真模型,實現這種轉變的計算方法主要有微分方程數值解法和離散相似法。
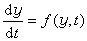
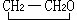
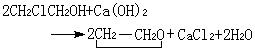
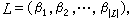
連續系統數字仿真方法是指用數字計算機對連續系統進行仿真的方法。採用這種方法時首先將連續系統的數學模型轉變為適合在數字計算機上進行試驗的仿真模型,實現這種轉變的...
根據仿真時所採用的計算機不同,可分為模擬仿真法、數字仿真法和混合仿真法三類。①模擬仿真法:採用模擬計算機對連續系統進行仿真的方法,主要包括建立模擬電路圖,確定...
《控制系統數字仿真》是北京理工年出版的圖書,作者是徐家蓓。...... 《控制系統數字仿真》介紹了連續系統和採樣系統的數字仿真原理和方法,《控制系統數字仿真》共分...
連續系統模擬仿真方法,用模擬計算機對連續系統進行仿真試驗的方法。採用模擬計算機來對這類系統進行仿真的方法有:柯西特徵法、分離變數法、線上求解法、有限差分法等...
連續系統模擬是建立連續系統的數學模型並形成電腦程式的模擬實驗。連續系統數字仿真一般採用數字積分器——數值積分算法或離散相似算法,以獲得較高的計算精度。常用的...
用混合計算機進行系統仿真的方法,有些複雜的連續系統仿真對計算精度和計算速度都有嚴格的要求。...
決策仿真是將仿真技術用於決策問題的方法。如將決策系統的決策因素、決策措施、決策目的等編成仿真程式,輸入計算機系統,以求得最佳解答。決策仿真的基本步驟是:(1)...
《控制系統數字仿真技術》是2007年8月中國電力出版社出版的圖書,作者是韓璞。...... 本書較為系統地介紹了控制系統的數字仿真原理及程式設計方法。對專用仿真程式設...
,過程系統模型化,連續系統的數字仿真,隨機噪聲的數字仿真,連續系統仿真與控制器參數最佳化,過程系統的仿真方法,基於仿真的過程系統的最佳化方法,過程計算機操作訓練仿真。...
的有效模型(數字的、物理效應的或數字物理效應混合的模型),並在模型上進行系統...由於連續系統和離散(事件)系統的數學模型有很大差別,所以系統仿真方法基本上分為...
50年代初,連續系統的仿真研究絕大多數是在模擬計算機上進行的。50年代中,人們開始利用數字計算機實現數字仿真。計算機仿真技術遂向模擬計算機仿真和數字計算機仿真兩個...
數字仿真語言是在FORTRAN語言基礎上開發的,用於連續系統數字仿真的數字仿真語言。由它編寫的面向數字仿真程式經過轉換成為FORTRAN子例程,然後對這些子例程重新組合後、...
《動力學系統數字仿真算法》是2000年科學出版社出版的圖書,作者劉德貴。...... 本書系統地論述了動力學系統數字仿真的概念、原理、方法以及構造仿真算法的基本思想和...
第一部分介紹控制系統計算機仿真的基本概念、仿真研究的步驟、控制系統仿真的數學模型和仿真軟體;第二部分介紹連續控制系統和採樣控制系統數字仿真的一些通用基本方法;第...
《控制系統數字仿真與CAD》是2011年機械工業出版社出版的圖書,作者是張曉華。...... 《控制系統數字仿真與CAD》是2011年機械工業出版社出版的圖書,作者是張曉華。...
第一部分介紹控制系統計算機仿真的基本概念、仿真研究的步驟、控制系統仿真的數學模型和仿真軟體;第二部分介紹連續控制系統和採樣控制系統數字仿真的一些通用基本方法;第...
《仿真技術與通信系統仿真》分四大部分介紹了數字仿真技術和通信系統仿真的原理和方法。第一部分介紹仿真技術的基本理論和方法,是《仿真技術與通信系統仿真》的重點...
《系統可靠性數字仿真》是北京航空航天大學出版社出版的一本書。...... 本書介紹了系統可靠性數字仿真方法。全書共分8章,主要內容包括:系統數字仿真概述,蒙特卡羅方...
《控制系統的數字仿真及計算機輔助設計》是2010年化學工業出版社出版的圖書,作者是錢積新、周立芳。...
本書介紹了計算機仿真技術基礎,系統模型建立的方法論,連續系統數值積分,離散事件系統仿真,面向對象的仿真,高層體系結構,嵌入式仿真系統與冷連軋最佳化仿真,仿真模型的校...
4.3 非線性系統的數字仿真方法4.4 連續系統按環節離散化的數字仿真程式本章小結習題第5章 採樣控制系統的數字仿真5.1 採樣控制系統..;...
5.4採樣控制系統的數字仿真方法程式及套用 第六章 面向方程的仿真語言 6.1連續系統仿真程式與仿真語言 6.2DARE-P仿真語言的特點與結構 6.3DARE-P的運行過程及套用...
第3章較詳細地介紹了連續系統的數字仿真,數學模型,數值計算方法,仿真程式,仿真程式包――CSS以及快速仿真程式。第4章介紹採樣系統數字仿真的原理、模型、程式及純...
《計算機仿真技術與套用》是由西北工業大學出版社於1998年2月出版的圖書。本書對系統仿真理論、技術以及仿真方法學、軟體和套用做了詳細的論述。...
4.3非線性系統的數字仿真方法4.4連續系統按環節離散化的數字仿真程式本章小結習題第5章採樣控制系統的數字仿真第6章動態仿真集成環境——Simulink...
本書對系統仿真理論、技術以及仿真方法學、仿真軟體和套用作了詳細的講述。主要內容有:系統仿真的基本概念、系統數學模型及其相互轉換、數值積分法在系統仿真中的套用...
本書從MATLAB仿真角度系統地介紹了PID控制的基本理論、基本方法和套用技術,是作者...[1] 全書共分10章,包括連續系統和離散系統的PID控制;常用數字PID控制;專家PID...
全書共分10章,內容包括緒論,仿真建模與模型變換,套用數值積分方法仿真連續系統,套用模型離散化方法仿真連續系統,特殊仿真模型的處理,計算機控制系統數字仿真,制導控制...
為給後續各章程式設計打下基礎,論述了自動控制系統的數字仿真方法;論述了經典的和現代的多種最佳化算法以及智慧型辨識方法,通過工程實例闡明了智慧型理論的實際套用方法等。...
