在一個排列中,如果一對數的前後位置與大小順序相反,即前面的數大於後面的數,那么它們就稱為一個逆序。 一個排列中所有逆序的總數叫做這個排列的逆序數。
基本介紹
定義
n級排列
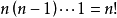
逆序
舉例
套用

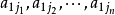



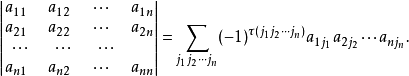


在一個排列中,如果一對數的前後位置與大小順序相反,即前面的數大於後面的數,那么它們就稱為一個逆序。 一個排列中所有逆序的總數叫做這個排列的逆序數。
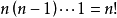

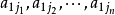



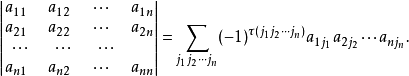


在一個排列中,如果一對數的前後位置與大小順序相反,即前面的數大於後面的數,那么它們就稱為一個逆序。 一個排列中所有逆序的總數叫做這個排列的逆序數。...
在一個排列中,如果一對數的前後位置與大小順序相反,即前面的數大於後面的數,那么它們就稱為一個逆序。一個排列中逆序的總數就稱為這個排列的逆序數。一個排列中...
如果存在正整數 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j],則 <A[i], A[j]> 這個有序對稱為A 的一個逆序對,也稱作逆序數。中文...
逆序解法是求解動態規劃問題的基本方法。尋找最優解的方向與多階段決策過程的實際行進方向相反,從最後一段開始計算逐段前推,求得全過程的最優策略。逆序解法和順序...
給定n個數1,2,...,n的一個排列a1a2...an,令bi是數i在此排列中的逆序數,換句話說,bi等於該排列中先於i又大於i的那些數的個數。數列b1b2...bn稱為...
逆序辭彙,就是將辭彙根據字母順序倒過來排列。通常大家背單詞都是按照正序方式背誦,但正序背誦有一個缺點,就是容易形成上下單詞的提示記憶。比如說背penitent(後悔的...
什麼是逆序列印一般情況下,在Word中列印文檔時會按照從前往後的順序進行列印。對於一些頁數較多的文檔,用戶常常需要按照從後往前的順序進行列印,即所謂的逆序列印。...
《現代漢語逆序詞典》是2011年9月1日華語教學出版社出版的圖書,作者是李菁民。...... 《現代漢語逆序詞典》嚴格按照國家語言文字規範標準編寫的綜合性語文詞典。根據...
《簡明逆序詞詞典》是山東教育出版社1999年出版的圖書。...... 圖集 簡明逆序詞詞典圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新:...
《英語辭彙逆序記憶手冊(第5版)》對部分核心辭彙輔之以經典的考題和長難句進行深入的分析,讓考生能鞏固對該詞的掌握和運用情況。做到記單詞與考試緊密結合,對考試...
《高考英語辭彙逆序突破》是2001年中國水利水電出版社出版的圖書,作者是文武。...... 《高考英語辭彙逆序突破》是2001年中國水利水電出版社出版的圖書,作者是文武。...
逆序法作圖(construction by reverse order)是與一般作圖程式相反的一種作圖方法,某些作圖題,需要在給定圖形上做出具體的符合某種性質的新圖形,如果這樣的圖形不易...
《最新考研英語辭彙逆序突破》是2012年2月出版的圖書,作者是黃淑琴。...... 《最新考研英語辭彙逆序突破》是2012年2月出版的圖書,作者是黃淑琴。作者 黃淑琴 ISB...
不過S2應做一下逆序處理。便可以按照逆波蘭式的計算方法計算了!逆波蘭式計算方法 編輯 新建一個表達式,如果當前字元為變數或者為數字,則壓棧,如果是運算符,則將...
《中古漢語同素逆序詞演變研究》是上海古籍出版社出版的圖書,作者是張巍。...... 《中古漢語同素逆序詞演變研究》是上海古籍出版社出版的圖書,作者是張巍。...
逆序數為奇數的排列稱為奇排列。經過一次對換,奇排列變成偶排列,偶排列變成奇排列。在全部n級排列中,奇、偶排列的個數相等,各有(n!/2 )個。任意一個n級排列...
正序第一種解釋謂五行相生的順序,第二的順序的一種,和逆序相反。...... 正序第一種解釋謂五行相生的順序 [1] ,第二的順序的一種,和逆序相反。...
位運算逆序 下面的程式讀入一個32位整數並輸出它的二進制倒序後所表示的數。輸入:1314520 (二進制為00000000000101000000111011011000)輸出:460335104 (二進制為...
在n個數碼1,2,…,n的全排列j1j2…jn中,若一個較大的數碼排在一個較小的數碼的前面,則稱它們構成反序,亦稱逆序,這個排列的所有反序的總和,稱為這個排列的...
亦稱“逆序詞典”。“正序詞典”的對稱。按照詞目的尾字、尾字母或尾音節為序編排的詞典。因尾部相同的詞語彙聚一起,便於查檢同詞尾的詞和同族詞,對構詞、構形...
