有些作圖題,需要在給定圖形上作出具有某種性質的新圖形,如果這樣的新圖形不易作出,那么可以首先在任意位置上按要求條件作出新圖形,然後再把這個新圖形移到給定圖形上,並使移動後保持圖形的契約性.這種作圖方法稱為逆序法或反求法。
基本介紹
- 中文名:逆序法作圖
- 外文名:construction by reverse order
- 別稱:反求法
- 所屬學科:數學(平面幾何)
- 簡介:與一般作圖程式相反的作圖方法
基本介紹,例題解析,
基本介紹
逆序法作圖(construction by reverse order)是與一般作圖程式相反的一種作圖方法,某些作圖題,需要在給定圖形上做出具體的符合某種性質的新圖形,如果這樣的圖形不易作出,那么可以首先在任意位置上按要求條件作出新圖形,然後再把這個新圖形移到給定圖形上,並使移動後保持圖形的契約。
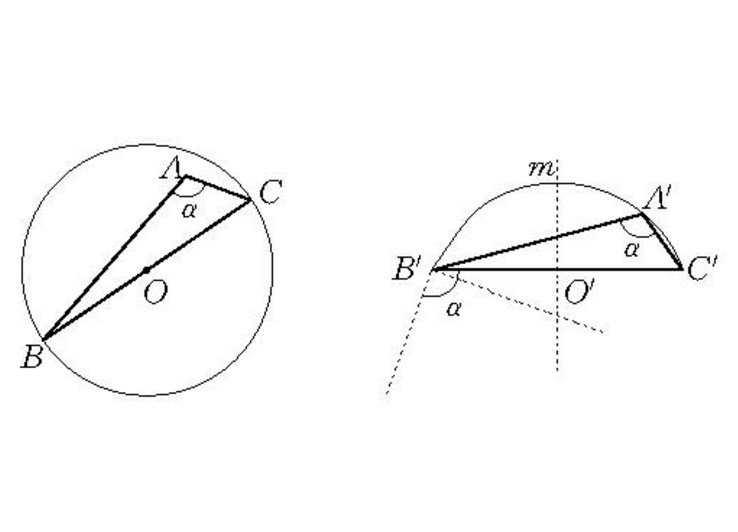
例如,在定圓中求作一直徑,使它對圓內已知點所張開的角等於已知角,其思路要點是:如圖,在⊙O內作一直徑BC,使它對圓內已知點A所張開的角等於已知角α,相當於已知底邊、頂角和底邊的中線作三角形,但由於頂點A是固定的,底邊是直徑,所以這個三角形的位置在⊙O內無法確定,然而,如果在任意位置上作出這樣的三角形,再將它移入⊙O內,是容易做到的,因此,本題採用逆序法作圖為宜,由於A點在⊙O內,所以α>90°,否則無解;若α>90°,當AO>h(弓形弧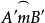 的高)時,△A′B′C′有兩解;當AO=h時,△A′B′C′有一解,在將△A′B′C′移入⊙O時,由於AB一般有兩解,因而符合條件的直徑BC的解數比△A′B′C′的解數要加倍。
的高)時,△A′B′C′有兩解;當AO=h時,△A′B′C′有一解,在將△A′B′C′移入⊙O時,由於AB一般有兩解,因而符合條件的直徑BC的解數比△A′B′C′的解數要加倍。
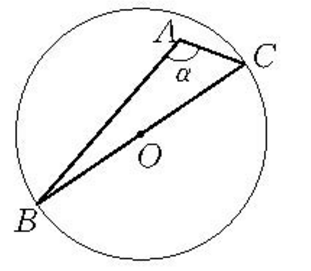 圖1
圖1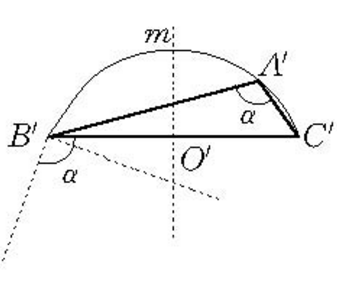 圖2
圖2例題解析
【例1】在定角XOY的兩邊上各求一點A、B,使AB等於定長l,而O與AB的距離等於定長h (圖3)。
分析:此問題實際上是要求在∠XOY上作一個三角形OAB,使它的一個角為∠XOY,對邊AB=l,AB上的高為h。在∠XOY上直接作這樣的三角形是非常困難的,因此,可採用逆序祛作圖,在任意位置上作一個這樣的三角形。然後再將這個三角形契約地移至∠XOY上。
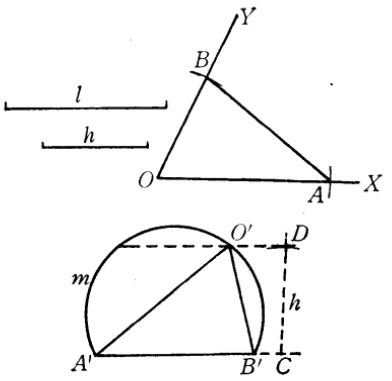 圖3
圖3作法:作弓形弧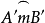 ,使弦A'B'=1,它所含的角等於∠XOY,作CD⊥A'B',垂足為C,使CD=h。過D作A'B'的平行線交弓形弧於O',連線A'O'、B'O'。
,使弦A'B'=1,它所含的角等於∠XOY,作CD⊥A'B',垂足為C,使CD=h。過D作A'B'的平行線交弓形弧於O',連線A'O'、B'O'。
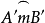
在∠XOY的邊OX上,取OA=O'A',在OY上, 取OB=O'B',連線AB,則A、B為所求兩點。
證明:根據作圖,△AOB≌△A'O'B’,則A'B'=AB=l,因為A' B'上的高為h,所以O到AB的距離為h,所以,A、B為所求兩點。
討論:過D作A' B'的平行線與弓形弧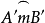 的交點有三種情況: (i)有兩個交點, 此時有兩解;(ii) 有一個交點,此時有一解;(iii)無交點,此時無解。
的交點有三種情況: (i)有兩個交點, 此時有兩解;(ii) 有一個交點,此時有一解;(iii)無交點,此時無解。
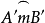
【例2】在定圓中求作一直徑,使它對圓內已知點所張開的角等於已知角(圖4)。
分析:假設直徑BC合乎條件, 連線AB、AC (A為O0內已知點),則∠BAC=a (已知角) .在△ABC中,BC、AO、∠BAC為已知,由此, 我們不難發現,在⊙O中作一直徑使它對圓內已知點A所張開的角等於已知角,相當於已知底邊、頂角和底邊上的中線作三角形。但頂點A是固定的,底邊又是直徑(過圓心),所以這個三角形的位置很難確定,然而,如果採用逆序法作圖,即在任意位置上作出這樣的三角形,再將它契約地移入⊙O內,是容易做到的。
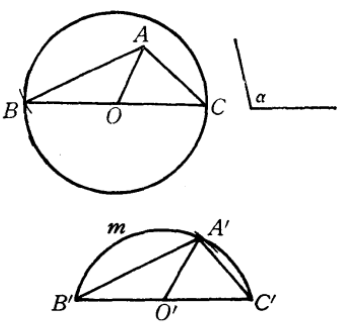 圖4
圖4作法:作以⊙O的直徑為弦,所含角等於α的弓形弧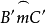 ,以B'C'的中點O'為圓心,以AO之長為半徑畫弧交弓形弧
,以B'C'的中點O'為圓心,以AO之長為半徑畫弧交弓形弧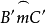 於A'。連線A'B'、A'C'。
於A'。連線A'B'、A'C'。
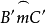
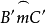
在⊙O內, 以A為圓心以A'B’為半徑畫弧交⊙O於B,連線BO並延長其交⊙O於C,BC即為所求直徑。
證明:連線AB、BC、CA、AO。由作圖△A'B'C'的底邊為⊙O的直徑,中線A'O'=AO,頂角A=a。
由作圖知,△ABO≌△A'B'O' (三對對應邊相等)。在△AOC與△A'O'C'中,AO= A'O',OC=O'C',
∵∠AOC=∠OBA+∠OAB, ∠A'O'C'=∠O'B'A'+∠O'A'B',
∵∠AOC=∠A'O'C',於是△AOC≌△A'O'C',
從而△ABC≌△A'B'C',所以BC為所求的直徑。
討論:由於A點在⊙O內,所以α>90°,否則本題無解。若α<90°,且當A0>h (弓形弧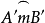 的高)時,△A'B'C'有兩解;當AO=h時,△A'B'C'有已解,當A0<h時,△A'B'C'無解,再將△A'B'C'契約地移入⊙O內時,由於AB一般有兩解,因而合條件的直徑BC的解數比△A'B'C'的解數相應地加倍。
的高)時,△A'B'C'有兩解;當AO=h時,△A'B'C'有已解,當A0<h時,△A'B'C'無解,再將△A'B'C'契約地移入⊙O內時,由於AB一般有兩解,因而合條件的直徑BC的解數比△A'B'C'的解數相應地加倍。
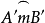
說明:逆序法不是什麼新的作圖方法,而是一種作圖的程式。它首先在任意位置按選定的作圖方法作出具有題中要求的滿足某條件的圖形,然後把這個圖形契約地移到題中指定的位置。這種作圖在程式上與正常作圖相反,因而稱為逆序法。