轉移機率矩陣(又叫躍遷矩陣,英文名:transition matrix)是俄國數學家馬爾科夫提出的,他在20世紀初發現:一個系統的某些因素在轉移中,第n次結果只受第n-1的結果影響,即只與當前所處狀態有關,而與過去狀態無關。 在馬爾科夫分析中,引入狀態轉移這個概念。所謂狀態是指客觀事物可能出現或存在的狀態;狀態轉移是指客觀事物由一種狀態轉移到另一種狀態的機率。
基本介紹
- 中文名:轉移矩陣
- 外文名:transition matrix
- 分類:數學
- 又名:躍遷矩陣
- 提出:馬爾科夫
- 相關:狀態轉移
簡介
特徵
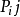
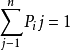
分析
舉例
明/今 | 晴 | 陰 | 雨 |
晴 | 3/4 | 1/2 | 1/4 |
陰 | 1/8 | 1/4 | 1/2 |
雨 | 1/8 | 1/4 | 1/4 |
 圖1.天氣轉移機率矩陣
圖1.天氣轉移機率矩陣