求和項是超幾何項的級數稱為超幾何級數。超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。
基本介紹
- 中文名:超幾何級數
- 外文名:hypergeometric series
- 適用範圍:數理科學
定義




超幾何項

雙超幾何項

正則超幾何項






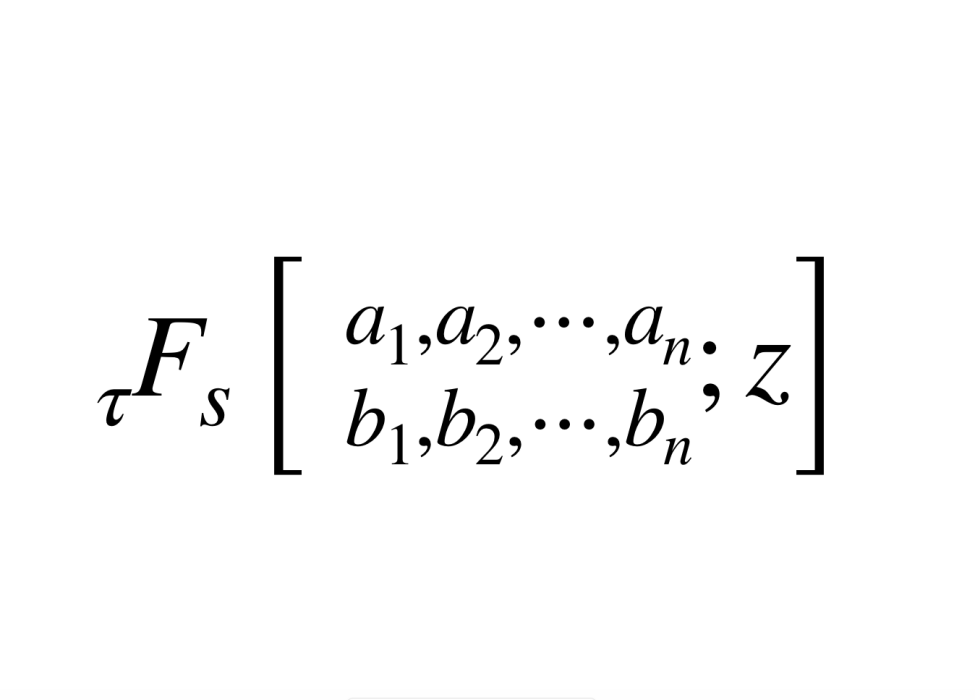
求和項是超幾何項的級數稱為超幾何級數。超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。












稱為超幾何分布,是因為其形式與“超幾何函式”的級數展式的係數有關。 [1] 超幾何分布中的參數是M,N,n,上述超幾何分布記作X~H(n,M,N) 。
高斯級數(Gauss series)即“超幾何級數”. [1] [1] 參考資料 1. 數學辭海 詞條標籤: 科學 圖集 高斯級數圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
庫默爾在數論、幾何學、函式論、數學分析、方程論等方面都有較大的貢獻,但最主要的是在函式論、數論和幾何三個方面。在函式論方面。他研究了超幾何級數,首次對...
第一類合流超幾何函式)M(a,b,z)是Kummer方程的解。注意有另一個相異且無關的函式也被稱為Kummer函式;V百科往期回顧 詞條統計 瀏覽次數:1788次 編輯次數:2...
合流超幾何函式(confluenthypergeometricfunction)定義為合流超幾何方程的解。它是高斯超幾何函式的極限情形,相當於超幾何方程中的兩個正則奇點1和∞合流為一個非...
托瑪級數 [1] (Thomae series )多參量情形下的一種推廣.(Thomae,L. J.)提出,定義為其中A為常數.超幾何級數是托瑪級數的特殊情形(m=2,n=1)....
我們利用一些數學工具和方法:選取適當收縮公式,利用發生函式與遞推關係,和角與差角的反正切公式,剩餘定理,使用微積分方法和複變函數方法,利用超幾何級數的求和公式...
4 超幾何級數和超幾何函式146 5 鄰次函式之間的關係148 6 超幾何方程的其他解用超幾何函式 表示151 7 指標差為整數時超幾何方程的第二解156 ...
洛默爾多項式 [1] (Lommel polynomial)是廣義超幾何函式的一種。洛默爾多項式 [1] (Lommel polynomial)廣義超幾何函式的一種.定義為
此外在橢圓函式、超幾何函式、發散級數等領域也有不少工作。他有較強的直覺洞察力,常能預見某些數學的結論,日後有許多得到了證實。1918年被選為英國皇家學會會員。
嫪麗切拉函式(Lauricella functions)是1893年義大利數學家Giuseppe Lauricella首先研究的三元超幾何函式。中文名 嫪麗切拉函式 外文名 Lauricella functions 研究時間 ...
在哈代和李特爾伍德等人的幫助下,拉馬努金進步很快,在素數分布、堆壘數論、廣義超幾何級數、橢圓函式、發散級數等領域取得了很多成果.他在歐洲的5年裡發表了21篇論文...
1 定義 2 級數展開 惠特克函式定義 編輯 惠特克函式,惠泰克1904推導合流超幾何函式,是下列惠泰克方程的解此方程在 有用正則奇點,在 有非正則奇點 [1] 。惠...
Battin利用超幾何級數法給出了經典Lambert問題的快速計算方法,趙瑞安對空間武器軌道設計中的經典Lambert問題進行了詳細介紹,並闡述了經典Lambert問題的Baton-Vaughan求解...
此後幾年之內,拉馬努金髮表了大量的研究成果,內容涉及素數分布理論、整數分拆、橢圓函式、超幾何函式、發散級數等許多領域 [1] 。 《知無涯者》巴西版海報 知無涯者...
庫默爾在數論、幾何學、函式論、數學分析、方程論等方面都有較大的貢獻,但最主要的是在函式論、數論和幾何三個方面。在函式論方面。他研究了超幾何級數,首次對...
在哈代和李特爾伍德等人的幫助下,拉馬努金進步很快,在素數分布、堆壘數論、廣義超幾何級數、橢圓函式、發散級數等領域取得了很多成果.他在歐洲的5年裡發表了21篇論文...
