洛默爾多項式(Lommel polynomial)是廣義超幾何函式的一種。
洛默爾多項式(Lommel polynomial)廣義超幾何函式的一種.定義為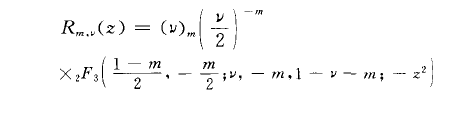
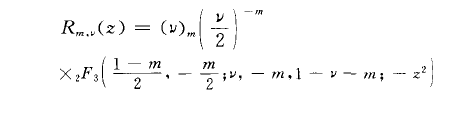
從而定義出洛默爾多項式,並給出了它的具體表達式.由於在推導這兩個關係式時只用到遞推關係,因此,如果將第一類貝塞爾函式換成其他柱函式,這兩個關係式仍然成立.
洛默爾多項式(Lommel polynomial)是廣義超幾何函式的一種。
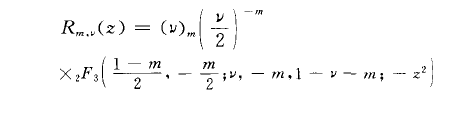
洛默爾多項式(Lommel polynomial)是廣義超幾何函式的一種。...... 洛默爾多項式[1] (Lommel polynomial)是廣義超幾何函式的一種。洛默爾多項式[1] (Lommel polynomial...
洛默爾函式(I,ommel function)非齊次貝塞爾微分方程的特解,Su.v(z}比Su.v (z)更常用,這是因為Su.v (z)在產+,或產一,為負奇數時無意義,但凡.v(z)無...
施勒夫利多項式(Schlafli polynomial)非齊次貝塞爾微分方程的解.即函式 其中On<t>為諾伊曼多項式.它們是洛默爾函式的特殊情形,施勒夫利多項式比諾伊曼多項式更常用,...
