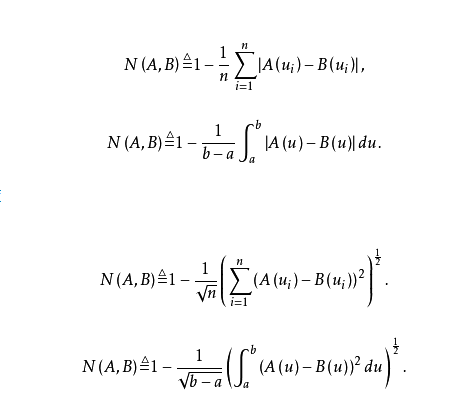貼近度

貼近度（nearness degree）是模糊數學的一個概念，它表示兩個模糊子集間相似程度的一種度量，它可以用於進行模式識別與情報檢索，也可以用於最佳化綜合判決中的權重。設F(X)表示論域X上的所有模糊集組成的集合，如果映射σ： F(X)×F(X)→[0，1]具有以下性質：1.σ(A，A)=1;2.σ(A，B)=σ(B，A);3.當A⊂B⊂C時，有σ(A，C)≤σ(B，C)，則稱σ為貼近度。符合上述條件的貼近度有各種不同的形式，可根據具體情況加以選用。設A₁，A₂，…，A_n是n個不同的模型，對於給定的B，若σ(B，A_i0)=max_i≤nσ(B，A_i)，則認為B與模型A_i0最貼近，這稱為擇近原則，它用於模式識別中。

基本介紹

• 中文名：貼近度
• 外文名：nearness degree
• 所屬學科：數學（模糊數學）
• 簡介：兩個模糊子集相似程度的一種度量

基本介紹

貼近度是對兩個F集接近程度的一種度量。

定義 設 ，若映射

滿足條件：

(1)

(2)

(3)若 ，則

則稱N(A，B)為F集A與B的貼近度。N稱為F(U)上的貼近度函式。

貼近度這個定義是原則性的概念，其具體規則視實際需要而定。

定理 若N(A，B)是模糊集合A與B間的貼近度，則 為A與B之間的距離。

兩個模糊集合之間的貼近度描述的是模糊集合之間的貼近度程度，兩個模糊集合之間的距離越大，說明離得越遠，貼近程度越小，貼近度越小；兩個模糊集合之間的距離越小，說明離得越近，貼近程度越大，貼近度也越大。

貼近度是模糊模式識別中一個重要的概念，在模糊模式識別中，按某種特性來比較兩個模糊集時，常用貼近度來表示比較的結果，即貼近度表示兩個模糊集接近的程度。目前貼近度已在模式識別、圖像處理、模糊控制等領域中有著廣泛的套用。它有各種形式，選擇不同的貼近度可以直接影響解決問題的效率。

幾種常見的貼近度

下面介紹幾種常見的類型：海明貼近度、歐幾里得貼近度、黎曼貼近度和格貼近度。

海明貼近度

若 ，則

當U為實數域上的閉區間 時，則有

歐幾里得貼近度

若 ，則

當 時，則有

黎曼貼近度

若U為實數域，被積函式為黎昌可積，日廣義積分收斂，則

格貼近度

格貼近度是有限論域上的F集表示為F向最的形式。