基本介紹
簡介
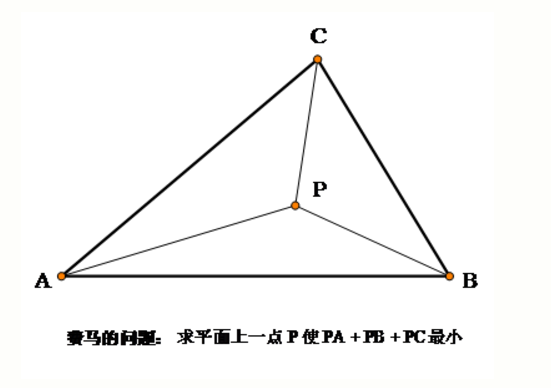
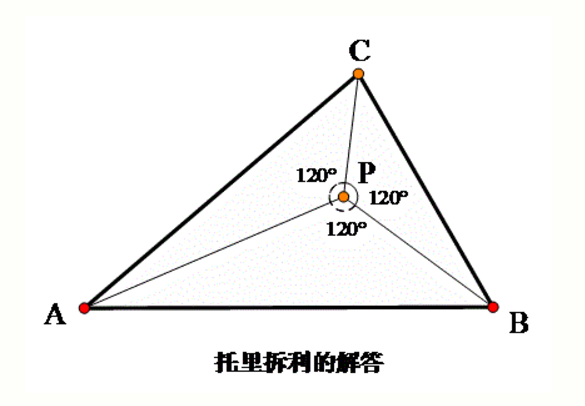
純幾何解法
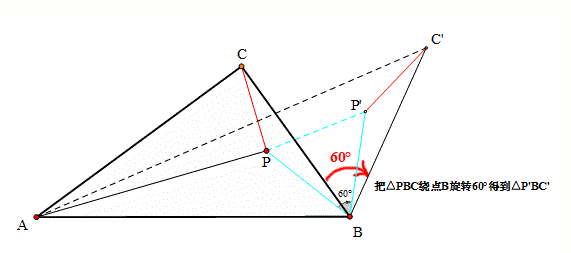
探討與證明
證明一
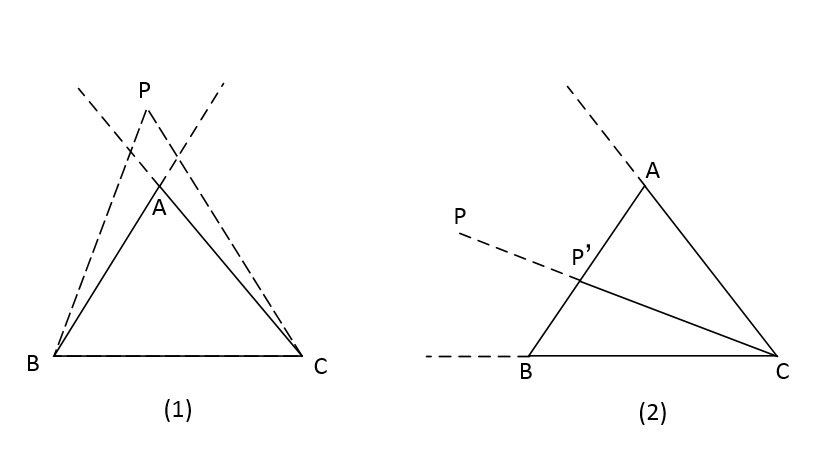
證明二
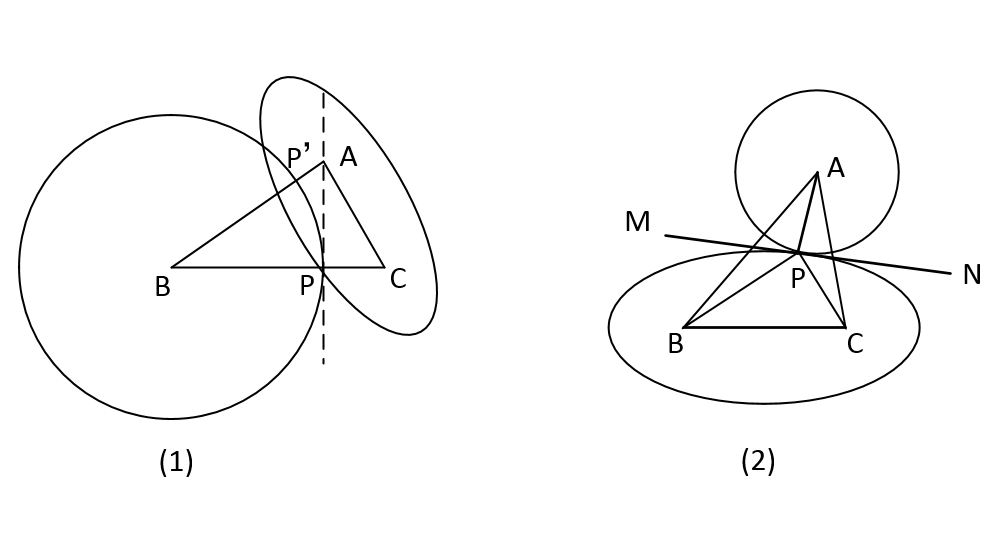
證明三
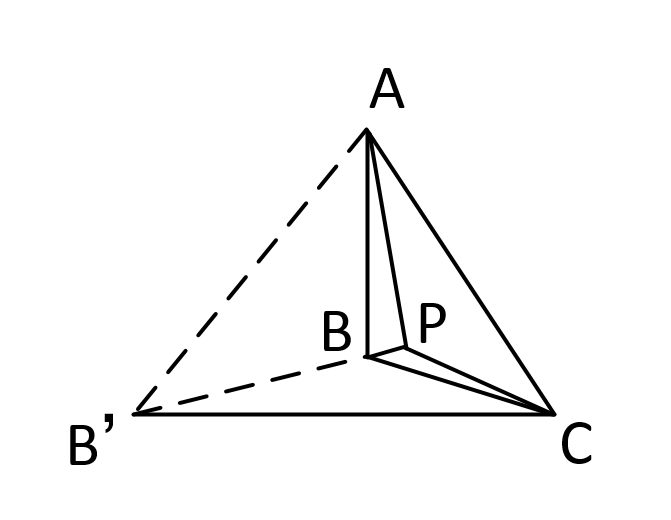
證明四
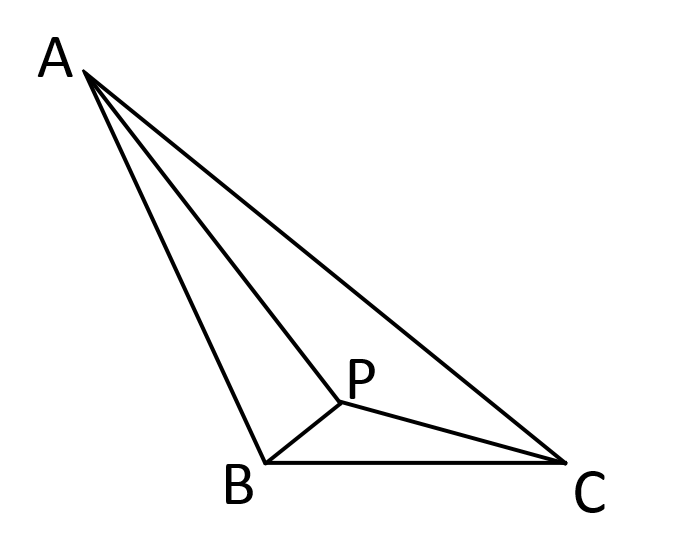







費馬問題(Fermat problem)是著名的幾何極值問題。費馬(Fermat , P. de)曾提出一問題征解:“已知一個三角形,求作一點,使其與這個三角形的三個頂點的距離之和為極小。”它的答案是:當三角形的三個角均...
費馬數問題(Fermat number problem)一種特殊結構的數的著名難題.數稱為費馬數.法國數學家費馬(Fermat , P. de )對n=0,1, 2, 3, 4的情形做了檢驗,發現此時F。都是素數.1640年,費馬給法國數學家梅森(Merse-nne, M.)寫信時...
而費馬多項式 沒有奇點,其虧格為 。當 時,費馬多項式滿足猜想的條件。因此,如果莫德爾猜想成立,那么費馬大定理中的方程 本質上最多有有限多個整數解。二戰後隨著計算機的出現,大量的計算已不再成為問題。藉助計算機的幫助,數學家們...
根據費馬原理:解之, 得 ,代入D得到:光程 ,乃是一個極大值=2.8R;(極小值光程是從直徑一端到Q另一端P,光程=2R)。運動學 伯努利家族的約翰·伯努利在解決最速降線問題時曾利用到費馬原理。他將小球運動類比作光線的運動...
)也就是說,所有具有形式 2ⁿ + 1 的素數必然是費馬數,這些素數稱為費馬素數。已知的費馬素數只有 F₀ 至 F₄ 五個。猜想 1640年,在數論領域留下不可磨滅足跡的費馬思考了一個問題:式子 的值是否一定為素數。當 n取0...
因此,利用費馬引理,求函式的極值的問題便化為解方程的問題。需要注意的是,費馬引理僅僅給出了可導函式在某個點為極值的必要條件。也就是說,有些駐點可以不是極值點,它們是拐點。要想知道一個駐點是不是極值點,並進一步區分極大...
第九章 55.童年時的夢想 56.重新點燃一個古老光焰 57.把一個大問題拆解為若干小問題 58.弗萊切的論文 59.一位好朋友 60.謎題的最後部分 61.檢驗 62.深藏的一個隱含的漏洞 63.煩惱 64.如願以償 第十章 65.費馬有證明嗎?
費馬點問題最早是由法國數學家皮埃爾·德·費馬在一封寫給義大利數學家埃萬傑利斯塔·托里拆利(氣壓計的發明者)的信中提出的。托里拆利最早解決了這個問題,而19世紀的數學家斯坦納重新發現了這個問題,並系統地進行了推廣,因此這個點也...
庫默爾在1844年提出了“理想數”概念,他證明了:對於所有小於100的素指數n,費馬大定理成立,此一研究告一階段。1849年德國數學家庫默爾,用近世代數的方法,引入自己發現的“理想數”的概念,指出費馬問題只可能在n等於某些值時,才有...
Open Problem就是所謂未解決的問題。而一個Open Problem有了解決方案後,就成為closed-ended question。在科學領域和數學領域,Open Problem一般是大家所公認的,準確提出的,尚未解決的問題。例如,非常著名的費馬大定理,由17世紀法國數學...
,則據費馬小定理知,n必為合數;如果n能整除 ,且n在偽素數表中,則n為合數,否則為素數。這種方法的關鍵就在於按偽素數表去掉偽素數,而這要求偽素數在能整除 的數中相當少才行,這就是當n整除 時,n是合數的比例問題。...
在數學及許多分支中都可以見到很多以歐拉命名的常數、公式和定理,得名於瑞士數學家萊昂哈德·歐拉。在數論中,歐拉定理(Euler Theorem,也稱費馬-歐拉定理或歐拉函式定理)是一個關於同餘的性質,實際上是費馬小定理的推廣。複數中的歐拉...
費馬的表述 1662年,皮埃爾·德·費馬提出費馬原理,又稱為“最短時間原理”:光線移動的路徑是需時最少的路徑。費馬原理更正確的版本應是“平穩時間原理”。對於某些狀況,光線移動的路徑所需的時間可能不是最小值,而是最大值,或...
,因而有b=x+y,c=xy。費馬然後考慮了一個重根,即x=y的情形,他發現:如此便求得問題的正確解,費馬認為他的方法是完全普遍的。內容 在《求極大值與極小值的方法》中,費馬將假定的兩個相異根記為A和A+E(即x和x+y),其...
1998年威爾斯因證實了17世紀法國數學家彼埃爾德·費馬的猜想而獲得了價值20萬美元的費薩爾國王獎。該問題將世界上最偉大的數學家們困擾了350年之久。在美國新澤西州普林斯頓大學任職的安德魯·威爾斯(英國)與費馬大定理的合影。
18世紀中葉,歐拉和其他數學家在解決物理問題的過程中,創立了微分方程這門學科。值得一提的是,關於偏微分方程的純數學研究的第一篇論文是歐拉寫的《方程的積分法研究》。歐拉還研究了用三角級數表示函式的方法和解微分方程的級數法等等...
物理學中泛函極值問題的提出促進了變分學的建立和發展,而變分學的理論成果則不斷滲透到物理學中。費馬原理 費馬原理指出:光沿所需時間為極值(極大值、恆值、極小值)的路徑傳播。假設 y=f(x)為光的路徑,則光程可以下式表示:...
1638年,法國數學家費馬在他所寫的一本關於求極值的書中就有了第一個問題,稱為費馬問題;第二個問題則到了18世紀中葉才由辛普森(A.R.Simpson)提出來。定義 斯坦納樹問題的定義隨著歷史的發展在不斷的擴展和推廣。瑞士數學家斯坦納...
1986年,格哈德·弗賴提出費馬大定理的真實性將是谷山—志村猜想一經證明之後的直接結果並演算出一個橢圓方程,於是,懷爾斯決定重新研究原來擱置的問題,並可以運用一些新的方法。經過7年的努力,懷爾斯完成了谷山—志村猜想的證明,同時也...
