基本介紹
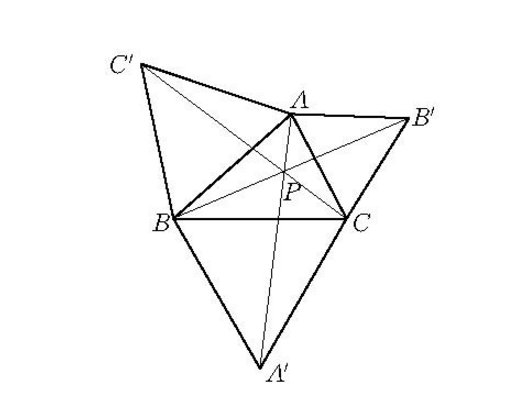
正等角中心(positive isogonal centre)亦稱費馬點,是三角形的巧合點之一。若分別以△ABC的三邊為邊,向形外作正三角形ABC′,BCA′,CAB′,則三直線AA′,BB′,CC′交於同一點P,並形成以P為頂點的六個相等的角,每個角等於60°(如圖1),點P稱為△ABC的正等角中心,當△ABC每個內角都小於120°時,正等角中心是到三頂點距離之和為最小的點,正等角中心早在古希臘時代已被發現,公元17世紀時,
費馬(Fermat,P.de)曾提出這樣的征解問題:求一點,使與定三角形三頂點的距離和為極小。因此,各角均小於120°的三角形的正等角中心又稱
費馬點。
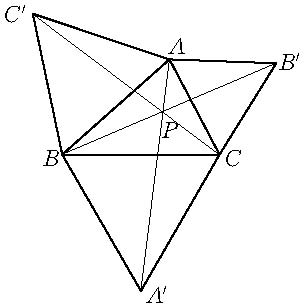 圖1
圖1正等角中心的證明
若在△ABC的外邊作正三角形△BCA'、△CAB'、△ABC' (圖2),則AA'、BB'、CC'三點共點。
 圖2(a)
圖2(a)這點叫做△ABC的
正等角中心,是三角形的巧合點之一,早在希臘時代已被發現。公元十七世紀時。法國數學家
費馬(Fermat,1601-1665年)曾提出一問題征解,問題是“求一點,使與定三角形三頂點的距離和為極小”。當三角形的三個角均小於120°的時候(圖2中),問題的解答正是三角形的正等角中心。因此各角均小於120°的三角形,它的正等角中心又有費馬點之稱。
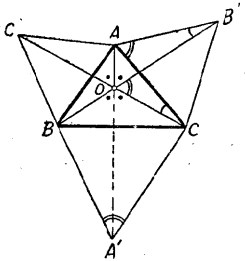 圖2(b)
圖2(b)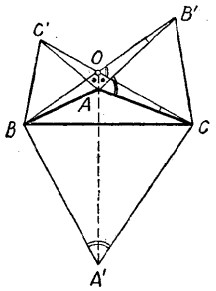 圖2(c)
圖2(c)題設 在△ABC的外邊作正三角形△BCA'、△CAB'、△ABC'。
題斷 AA'、BB'、CC" 三線共點。
思索方法 在AA'、 BB'、CC'三線中,如果其中兩線的交點是△ABC的頂點之一(當△ABC有一角等於120°時),則問題已顯而易見。現在假定BB'與CC'的交點是O,連OA和OA'。 由題設,易知△ABB'與△AC'C
契約,因而A與BB'、C'C等距。那么OA是∠B'OC'或∠BOC的平分線(就圖2來看)。於是若能證OA'是∠BOC的平分線,問題便解決了。為要考究這一點,我們想到圖形中有許多60°的角,應該設法利用它們。從上述兩個契約三角形的對應角相等這個關係看來,我們馬上發覺∠COB'= ∠CAB'= 60°, 由此可見O、B、A'、C四點同在一圓上。這就證實了我們剛才的希望沒有落空。
證明分三種情形證明如下:
1° 假定△ABC有一角例如A角等於120° (圖2(a))。這時BAB'與CAC'顯然都是直線,因而AA'、BB'、CC'三線會於A點是十分明白的。
2° 假定△ABC各角均小於120° (圖2(b))。這時BB'、CC'兩線顯然交於△ABC內部一點O,連OA和OA'。由題設,AB= AC',AB'= AC,且
∠BAB'=∠BAC+∠CAB'=∠BAC+∠C'AB=∠C'AC,
故 △ABB'≌△AC'C。
由此得知A與BB'、C'C等距,那么OA是∠B'OC'的平分線。
在契約三角形△ABB'與△AC'C中,有∠AB'O=∠ACO。因此A、B'、C、O四點同在一圓上,從而∠COB'= ∠CAB'= 60°。但據題設,∠CA'B= 60°,可見四邊形OBA'C有外接圓。這樣一來,由A'B=A'C,便知OA'是∠BOC的平分線。
以上的結果,證明了A、O、A'三點是共線的。這就是說,AA'、BB'、CC'三線會於O點。
3° 假定△ABC有一角例如A角大於120° (圖2(c))。這時BB'、CC'兩線將交於△ABC外部一點O(O、A同在BC的一側),連OA和OA'。仿上面的步驟,可以證明,△ABB'與△AC'C契約及四邊形OBA'C有
外接圓,因此OA,OA'同為∠BOC的平分線。於是OA和OA'必然合而為一,所以題斷成立。
 圖1
圖1 圖2(a)
圖2(a) 圖2(b)
圖2(b) 圖2(c)
圖2(c)