負等角中心

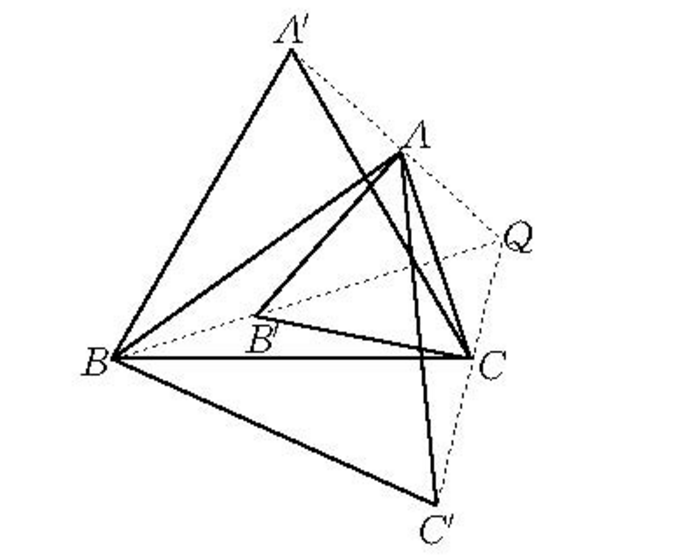
負等角中心(negative isogonal centre)是三角形的巧合點之一。若△ABC不是正三角形，分別以三邊為邊向△ABC內側作三個正三角形：△ABC′，△BCA′和△CAB′，則三直線AA′，BB′，CC′交於同一點Q，點Q稱為△ABC的負等角中心。

基本介紹

• 中文名：負等角中心
• 外文名：negative isogonal centre
• 所屬學科：數學
• 所屬問題：平面幾何（三角形）

基本概念

正等角中心

在△ABC的外邊作正三角形△BCA'、△CAB'、△ABC'，AA'、BB'、CC'必共點，這點稱為△ABC的正等角中心。

當△ABC的各角均小於120°時，正等角中心O在△ABC形內，且∠BOC=∠COA=∠AOB=120°；

當各角中有一個角(例如∠A)等於120°時，則O與A重合；

當∠A>120°，則O在△ABC形外(O、A同在BC一側)，且∠BOC=120°，∠COA=∠AOB=60°。

負等角中心

在△ABC的內側作正三角形△BCA'、△CAB'、△ABC'，AA'、BB'、 CC'也必共點。這點叫做△ABC的負等角中心。

當△ABC有一個角(例如∠A)等於60°時，負等角中心O'與A重合；

當△ABC只有一個角(例如∠A)大於60°，且∠B、∠C均不等於60°，負等角中心O'在△ABC形外(O'、A在BC兩側)，且∠BO'C=120°，∠CO'A=∠AO'B=60°；

當△ABC有兩個角(例如∠B和∠C)大於60°，負等角中心O'亦在△ABC形外(O'、A在BC兩側)，同樣有∠BO'C=120°，∠CO'A=∠AO'B=60°，△ABC不能為等邊三角形，因此此時O'不存在。

等角中心問題的研究始於十七世紀的歐洲，當時法國數學家費爾馬提出問題征解:“求一點，使此點至三定點之距離和為極小”，當上述三定點所決定的三角形的各內角均小於120°時，解答正是三角形的正等角中心。故各角均小於120°的三角形的正等角中心又稱費爾馬點。

負等角中心的證明

已知 以△ABC的每邊向內側作正三角形ABD、BCF和ACE 。

求證 ⊙ABD，⊙BCF及⊙ACE相交於一點。

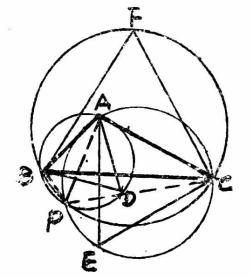圖6

證明 設⊙ABD和⊙ACE相交於點P，連結PB，PA，PC。

在⊙ABD中∠APB=∠ADB= 60°，

在⊙ACE中∠APC=∠AEC= 60°，

因為同弧上的圓周角相等，

所以∠APB+∠APC=120°，

即∠APC+∠F =120°+ 60°= 180°，

所以F, B, P, C四點共圓。

故以上三圓共點。

此點叫做原三角形的負等角中心。