費勒過程(Feller process)是一類馬爾可夫過程,指其對應的轉移運算元把連續函式映為連續函式的馬爾可夫過程.設E為距離空間,省為E上開集產生的。
基本介紹
- 中文名:費勒過程
- 外文名:Feller process
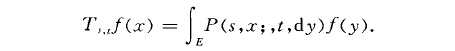
費勒過程(Feller process)是一類馬爾可夫過程,指其對應的轉移運算元把連續函式映為連續函式的馬爾可夫過程.設E為距離空間,省為E上開集產生的。
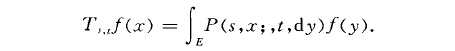
費勒過程(Feller process)是一類馬爾可夫過程,指其對應的轉移運算元把連續函式映為連續函式的馬爾可夫過程.設E為距離空間,省為E上開集產生的。代數,C為定義在E上連續函式的全體.如果ds<t,若fEC,有...
最小Q過程是(minimal 62-process)滿足某種附加條件的Q過程。在Q過程的存在性和惟一性問題的研究中,南斯拉夫一美國數學家費勒(Feller, W.F.)於1940年首先通過構造一個最小Q過程,解決了是否存在對應於給定Q矩陣的Q過程的問題.美國數學...
費勒在生滅過程、隨機泛函、可列馬爾可夫過程積分型泛函的分布、布朗運動與位勢、超過程等方向上均成就斐然,對近代機率論的發展作出了卓越的貢獻。他是權威數學雜誌德國和美國《數學評論》的創始人和第一位主編。榮譽 費勒曾經擔任國際...
在擴散過程中,費勒引進了一般微分運算元。費勒還從機率論的角度出發,對中的拉普拉斯運算元以及與它相類似的運算元,研究了使之成為正定半群的生成運算元的最小運算元的擴張,他還把這一結果向多維空間推廣,作了種種探索.費勒將機率論套用於...
《心理諮詢的過程》是2009年4月高等教育出版社出版的圖書,作者是韋爾費勒。內容簡介 《心理諮詢的過程——多元理論取向的整合探索(第6版)》準確地把握了這個趨勢。《心理諮詢的過程——多元理論取向的整合探索(第6版)》既提供了心理...
馬爾可夫過程理論的進一步發展表明,強馬爾可夫過程才是馬爾可夫過程真正研究的對象。歷史 1951年前後,伊藤清建立的隨機微分方程的理論,為馬爾可夫過程的研究開闢了新的道路。1954年前後,W.費勒將半群方法引入馬爾可夫過程的研究。流形上的...
伽馬過程(Gamma Process)是隨機過程理論中一類重要過程Lévy過程的一種,其增量服從獨立的gamma分布,可以用於描述單調遞增的變化過程,屬於Lévy subordinator中的一種。gamma過程,通常記作 ,由兩個正參數決定,其中 稱為形狀參數,控制...
1951年前後,日本數學家伊藤清在法國數學家萊維和原蘇聯數學家伯恩斯坦等人工作的基礎上,建立了隨機微分方程理論,為研究馬爾可夫過程開闢了新的途徑。1954年前後,南斯拉夫—美國數學家費勒將泛函分析中的半群方法引入馬爾可夫過程的研究中,...
在數學中以他的姓氏命名的有:費勒過程、費勒鏈、費勒半群等等。編輯推薦 本書是威廉·費勒的著作《機率論及其套用》第1卷的續篇。曾經影響了包括中國在內的世界各國幾代機率論及其相關領域的學生和研究者。即使用今天的標準來衡量,...
[美]威廉.費勒(1907年7月1日—1970年1月14日),克羅地亞裔美國數學家,20世紀最偉大的機率學家之一。師從著名數學家希爾伯特和柯朗,年僅20歲就獲得哥廷根大學的博士學位。在生滅過程、隨機泛函、可列馬爾可夫過程積分型泛函的分布、...
費勒(FelIer)初等更新定理 記 ,則 ,若 ,則 。布萊克韋爾(Blackwell)更新定理 記 ,有:(1) 若F不是格點的,則對一切 ,當 時有 。(2) 若F是格點的,周期為d,則當 時,有P{在nd處發生更新)。關鍵更新定理(史密斯(...
《機率論及其套用·第二卷》是1994年科學出版社出版的圖書,作者是(美)費勒(Feller, William)。內容簡介 本書介紹各種重要的分布和隨機過程,討論大數定律、中心極限定理和無窮可分分布,更新理論及調和分析等。圖書目錄 第一版序 引...
第 12 章 複合分布·分支過程 第 13 章 循環事件·更新理論 第 14 章 隨機遊走與破產問題 第 15 章 馬爾可夫鏈 第 16 章 有限馬爾可夫鏈的代數處理 第 17 章 簡單的依時的隨機過程 習題解答 作者簡介 威廉·費勒(1906—...
W.費勒的原書第一卷討論離散樣本空間中的機率問題,取材很廣.中譯本分上下兩冊出版,上冊(包括原書第一卷一至九章)包含了機率論的基本內容,下冊(包括原書第一卷十至十七章)包含大數定律、取整數值的隨機變數與母函式、分支過...
