基本介紹
- 中文名:負數表示法
- 外文名:negative number representation
- 符號位:用1表示
- 表示方法:原碼、反碼、補碼
- 類型:十進制數
- 套用學科:計算機原理
原碼


補碼




反碼


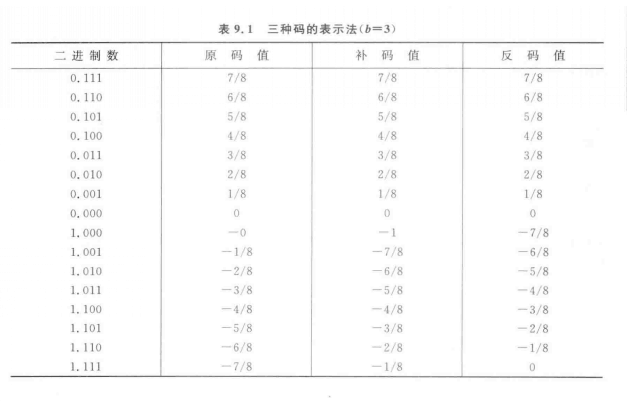









對於負數,根據需要的不同,有原碼、反碼、補碼三種表示方法。原碼 原碼也稱“符號——幅度碼”,它的尾數部分代表數的絕對值(即幅度大小),符號位代表數的正負號, 是代表正數, 時代表負數,例如x=0.011表示的是+0.375,x=1.011表示的是一0.375。原碼的優點是乘除運算方便.以兩數符號位的邏輯加就可簡單...
負數是由中國古代的數學家最先所採用及套用的,在《九章算術》中便記載了負數及負數的運算法則。而在其他運\算中,亦有不同的方式來表示正負數,如在籌算時,會以紅色的籌表示正數,黑色的籌表示負數。但這種方法用於毛筆記錄時,換色十分不便,因此在12世紀,李冶首創了在數字上加斜劃以表示負數(見圖一)。...
,負號表示動能減少了。 (4)對正、負號的特別規定。例如:電源電動勢的方向規定為從電源負極經內電路指向正極;磁通量的正、負;熱力學第一定律△U=W+P中,P為正表示氣體吸熱,P為負表示氣體放熱;W為正,表示外界對氣體做功,平為負,表示氣體對外界做功。 [2] ...
5、用搜狗輸入法或百度輸入法輸入“zhengfu”即可。物理學中 正負號在中學物理中不是單一的概念,可以用來表示有理數的正負,有的則用來表示物理量的性質、方向,情況較為複雜。學生到了高中的最後階段,隨著知識的積累,往往會形成負遷移,造成物理量的正負方面錯誤百出。有以下幾種表現:1、將物理的正負簡單理解為...
用一位二進制位表示數的符號:0表示正數,1表示負數,這種表示數的方法,稱為帶符號數的表示方法。所表示的數,叫做帶符號的數。帶符號的數其最高位為符號位。如果將全部有效位都用來表示數的大小,這種數的表示方法,叫無符號數的表示方法,所表示的數,叫無符號數。真值與機器數 真值就是利用"+"、"-"表示...
最負的數 最負的數是位數的二進制數中絕對值最大的負數。“最負的數”通常在計算機領域裡使用,主要是指用補碼、原碼、反碼等表示方法來表示的一定位數的二進制數中絕對值最大的負數
在普通套用中,-0有可能被用來表示一個可以四捨五入為零的負數,或者是一個從負方向上趨近於零的數。在統計力學中,特定的系統在反轉分布的狀態下,可以被認為擁有-0的絕對溫度。表示法 在對於整數的1+7比特的符號數值表示法中,負零是用二進制代碼10000000表示的。在8比特二進制反碼中,負零是用二進制代碼...
相反數是一個數學術語,指絕對值相等,正負號相反的兩個數互為相反數。相反數的性質是他們的絕對值相同。例如:-2與+2互為相反數。用字母表示a與-a是相反數,0的相反數是0。這裡a便是任意一個數,可以是正數、負數,也可以是0。基本含義 基本概念 相反數(opposite number)1、相反數特性:若a.b互為相反數...
在計算機內,有符號數有3種表示法:原碼、反碼和補碼。詳細釋義 所謂原碼就是二進制定點表示法,即最高位為符號位,“0”表示正,“1”表示負,其餘位表示數值的大小。反碼錶示法規定:正數的反碼與其原碼相同;負數的反碼是對其原碼逐位取反,但符號位除外。原碼10010= 反碼11101 (10010,1為符號碼,故為負)...
(3)負數補碼錶示的範圍比原碼稍寬,多一種數碼組合。對於定點數,若為純小數,表示範圍為:,若為純整數,表示範圍為:。原碼求補碼 求給定數值的補碼分以下兩種情況:正數 正整數的補碼是其二進制表示,與原碼相同。例:+9的補碼是00001001。(備註:這個+9的補碼是用8位2進制來表示的,補碼表示方式很多,還有...
16世紀義大利米蘭學者卡爾達諾(Jerome Cardan,1501年~1576年)在1545年發表的《重要的藝術》一書中,公布了一元三次方程的一般解法,被後人稱之為“卡當公式”。他是第一個把負數的平方根寫到公式中的數學家,並且在討論是否可能把10分成兩部分,使它們的乘積等於40時,他把答案寫成 ,儘管他認為和這兩個表示式...
其中,符號位為0,表示其後的BCD數為負。另一種表示法就是用58相對某一數值範圍的最大BCD數的補碼來表示。如果在所考慮的數值範圍內最大數為100(一百),那么,一58可用42來表示,即:一0101 1000——→0100 0010 轉換的規則如下:表示負值的正數相對原負數而言,其最低位BCD數應取BCD補碼,其餘各位BCD數應取...
在計算機內,有符號數有3種表示法:原碼、反碼和補碼。幾種表示法關係密不可分。原碼 原碼是計算機機器數中最簡單的一種形式,數值位就是真值的絕對值,符號位為“0”時表示正數,符號位為“1”時表示負數,原碼又稱帶符號的絕對值。為了方便整數和小數區別,整數的符號位與數值位之間用“,”隔開,小數的符號...
在做除法運算時,根據同號得正,異號得負的法則先確定符號,再把絕對值相除。若在算式中帶有帶分數,一般先化成假分數進行計算。若不能整除,則除法運算都轉化為乘法運算。乘方運算 1、負數的奇數次冪是負數,負數的偶數次冪是正數。例如:(-2)³(-2的3次方)=-8,(-2)²(-2的2次方)=4。2、...
阿拉伯數字由0,1,2,3,4,5,6,7,8,9共十個計數符號組成。採取位值法,高位在左,低位在右,從左往右書寫。藉助一些簡單的數學符號(小數點、負號、百分號等),這個系統可以明確的表示所有的有理數。為了表示極大或極小的數字,人們在阿拉伯數字的基礎上創造了科學記數法。歷史 起源 公元500年前後,...
例如,一個指數範圍為±4的4位十進制浮點數可以用來表示43210,4.321或0.0004321,但是沒有足夠的精度來表示432.123和43212.3(必須近似為432.1和43210)。當然,實際使用的位數通常遠大於4。特別數值 此外,浮點數表示法通常還包括一些特別的數值:+∞和−∞(正負無窮大)以及NaN('Not a Number')。無窮大...
這時就用一條規定了原點、正方向和單位長度的直線來表示實數。規定右邊為正方向時,在這條直線上的兩個數,右邊上點表示的數總大於左邊上點表示的數,正數大於零,零大於負數。簡介 直線是由無數個點組成的集合,實數包括正實數、零、負實數也有無數個。正因為它們的這個共性,所以用直線上無數個點來表示實數。
負算 負算(Fusuan)中國古算術語.中國古代表示負數的算籌.在《九章算術》劉徽注文中說:以黑色籌為負,或斜放一籌表示負算(參見“正算”).
實數可實現的基本運算有加、減、乘、除、乘方等,對非負數(即正數和0)還可以進行開方運算。實數加、減、乘、除(除數不為零)、平方後結果還是實數。任何實數都可以開奇次方,結果仍是實數,只有非負實數,才能開偶次方其結果還是實數。性質 封閉性 實數集對加、減、乘、除(除數不為零)四則運算具有封閉...
將數的真值形式中“+”號用“0”表示,“-”號用“1”表示時,叫做數的原碼形式,簡稱原碼。若字長為n位,原碼一般可表示為:當X為正數時[X]原和X一樣,即[X]原 = X。當X為負數時 。由於X本身為負數,所以,實際上是將∣X∣數值部分絕對值前面的符號位上寫成“1”即可。原碼表示法比較直觀,它的數值...
