基本介紹
- 中文名:貝葉斯區間估計
- 外文名:Bayesian interval estimation
- 所屬學科:數學
- 相關概念:置信度、後驗分布、置信區間等
基本介紹







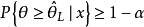
的













最大後驗密度可信區間

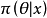

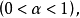



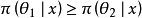













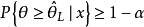














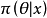

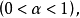



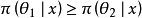





貝葉斯區間估計比經典的區間估計更容易處理,因為參數是隨機變數,對給定置信度1-α,利用θ的後驗分布可以較方便地求得θ的置信區間。...
區間估計(interval estimate)是在點估計的基礎上,給出總體參數估計的一個區間範圍,該區間通常由樣本統計量加減估計誤差得到。與點估計不同,進行區間估計時,根據樣本...
貝葉斯置信區間 英文名為 en:Credible Interval[1],有時也簡稱為置信區間。給定一定的實驗(測量)結果,通過貝葉斯的理論可以計算出被估計參數的後驗機率分布,從而...
估計分為點估計和區間估計。點估計,是根據觀測值估計出對母體 參數θ的估計值T...2. 李瑋軍,孟昭為.變參數貝葉斯先驗估計[J].重慶理工大學學報(自然科學),2015...
參數估計(parameter estimation),統計推斷的一種。根據從總體中抽取的隨機樣本來估計總體分布中未知參數的過程。從估計形式看,區分為點估計與區間估計:從構造估計量的...
預測區間即預先推測或測定任何的連續塊,除了點預測外還有另外一類預測問題,即...Zeller 線上性一指數損失函式下討論了貝葉斯估計與預測問題,並且得到了非常好的...
4.3.4線上性損失函式下的貝葉斯估計 4.4假設檢驗和有限行動(分類)問題 4.4.1假設檢驗問題 4.4.2多行動問題(分類問題) 4.4.3統計決策中的區間估計問題 4.5...
常用方法有:矩估計法、極大似然估計法、最小二乘法、貝葉斯估計法。區間估計(置信區間的估計):依據抽取的樣本,根據一定的正確度與精確度的要求,構造出適當的區間...
1.8 信號參量估計基本理論1.8.1 經典估計1.8.2 貝葉斯估計1.8.3 最大後驗估計...1.9.2 單個母體的區間估計本章小結習題一第2章 高斯信道中確知信號的檢測...
提出本文觀點:信用風險分析的本質是處理不確定性,而關鍵是貝葉斯統計決策方法的...查常態分配表,UP =C,則初級償債來源均值μ的區間估計為[μ″-C*S,μ″+C...
貝葉斯學派認為:這個後驗分布綜合了樣本X及先驗分布π(θ)所提供的有關的信息...為作θ的區間估計,可以取區間[A(X),B(X)],使π(A(X)≤θ≤B(X)│X...
第2章目標識別機率估計 2.1引言 2.2經典統計估計方法 2.2.1點估計值法 2.2.2區間估計法 2.3貝葉斯分析估計法 2.3.1區間類型 2.3.2估計準則...
