基本介紹
- 中文名:證明論
- 外文名:Proof theory
- 類別:數學理論
- 本質:語法邏輯
基本方法
表系統
序分析
發展歷史
亞結構邏輯






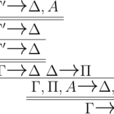






證明論(Proof theory),是數理邏輯的一個分支,它將數學證明表達為形式化的數學客體,從而通過數學技術來簡化對他們的分析。證明通常用歸納式地定義的數據結構來表達,...
在數學上,證明是在一個特定的公理系統中,根據一定的規則或標準,由公理和定理推導出某些命題的過程。...
理論論證是一種議論文中的論證方法,又叫演繹論證。演繹論證(理論論證)是根據一般原理或結論來論證個別事例的方法。即用普遍性的論據來證明特殊性的論點。...
獨立證明,通過論證與被反駁命題具有矛盾關係或反對關係的命題的真實性,從而確定被反駁命題虛假的反駁方法。間接反駁需要先設立一個與被反駁論題相矛盾或反對的論題,...
惡魔的證明原本的出處是拉丁文probato diablolica(devil's proof),這是一個在修辭學以及詭辯術上經常被使用的招數。...
論證,漢語詞語,同時也是哲學用詞。(1) 用論據證明論題的真實性對哥白尼的假說加以論證並使之通俗化(2)根據個人的了解或理解證明公誼會的教徒們長期以來都在論證...
論據,漢語辭彙,讀音lùnjù。意思是(1) 邏輯學指用來證明論點的判斷。(2)它是議論文三要素中的1種。(3) 理論的根據(多指事實)。
舉例論證法——例舉確鑿的事例來證明論點.道理論證法——以闡述道理的方式來證明論.比喻論證法——用淺近的並為人們熟識的事物作比喻來證明論點....
可計算論,是一個數理邏輯分支,起源於可計算函式和圖靈度的研究,其領域增長為包括一般性的可計算性和可定義性的研究。在這些領域中,這門理論同證明論和能行描述...
循環論證(又稱為乞詞魔術等),用來證明論題的論據本身的真實性要依靠論題來證明的邏輯錯誤。如證明“鴉片能催眠”,所用的論據是“它有催眠的力量”。而“鴉片有...
針對客觀事物或問題,直接提出自己的見解和主張,闡明其理由,表明自己的態度就是立論。換一個角度來說,立論就是運用充分有力的證據從正面直接證明自己論點正確性的...
有的文章,首先證明與論敵的論點相對立的論點是正確的,以此來證明論敵的論點是錯誤的。②通過批駁對方的論據來駁倒對方的論點。論據是論點的根據,是證明論點的。...
舉例論證,是指運用典型事例來證明論點的方法。通過列舉典型事例,具體有力地證明了中心論點,增強了說服力。...
類比論證是一種通過已知事物(或事例)與跟它有某些相同特點的事物(或事例)進行比較類推從而證明論點的論證方法。其中,“相同特點”是這種論證方法能夠成立的前提,沒...
這有力地證明的懷疑主義的重要作用(即使是極端的懷疑主義),而我們哲學界對於這...通過以上的考察與分析,我們看到,哲學中有兩種有著本質區別的懷疑主義:不可知論...
可實現性是可用來處理關於公式的信息而不是關於公式的證明的那部分證明論。自然數n被稱為實現了自然數算術的語言中一個陳述。其他邏輯和數學陳述也是可實現的,假如...
3、對比論證:拿正反兩方面的論點或論據作對比並在對比中證明論點。4、比喻論證:用人們熟知的事物作比喻來證明論點。5、象徵論證:用物體象徵來證明論點。...
類比論證是一種通過已知事物(或事例)與跟它有某些相同特點的事物(或事例)進行比較類推,從而證明論點的論證方法。...
要證明一個理論的判定問題是不可解的,首先需要把算法(機械程式)概念精確化,並...它包括邏輯演算(命題演算與謂詞演算)、公理化集合論、證明論、遞歸函式論、模型...
用經典著作中的精闢見解,古今中外名人的名言警句以及人們公認的定理公式等來證明論點。...
