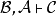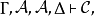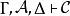證明論

證明論（Proof theory），是數理邏輯的一個分支，它將數學證明表達為形式化的數學客體，從而通過數學技術來簡化對他們的分析。證明通常用歸納式地定義的數據結構來表達，例如鍊表，盒鍊表，或者樹，它們根據邏輯系統的公理和推理規則構造。因此，證明論本質上是語法邏輯，和本質上是語義學的模型論形相反。和模型論，公理化集合論，以及遞歸論一起，證明論被稱為數學基礎的四大支柱之一。

證明論也可視為哲學邏輯的分支，其主要興趣在於證明論語義學的思想，該思想依賴於結構證明論的技術型想法才可行。

基本介紹

• 中文名：證明論
• 外文名：Proof theory
• 類別：數學理論
• 本質：語法邏輯

基本方法

表系統使用結構證明論的解析證明的中心思想來為一大類的邏輯提供決策或者準決策進程。序分析是為形式化算術和分析的理論提供組合式自洽性證明的有力技術。

表系統

表系統使用結構證明論的解析證明的中心思想來為一大類的邏輯提供決策或者準決策進程。

序分析

序分析是為形式化算術和分析的理論提供組合式自洽性證明的有力技術。

發展歷史

數學中的證明一向是邏輯學家研究的對象，但證明論是數學家D.希爾伯特於20世紀初期建立的，目的是要證明公理系統的無矛盾性，希爾伯特提出一整套嚴格的方案，規定只能用有限長的證明，要無可辯駁地給出整個數學的無矛盾性。他打算先給出公理化的算術系統的無矛盾性，再證明數學分析，集合論的無矛盾性。但1931年，K.哥德爾證明：一個包含公理化的算術的系統中不能證明它自身的無矛盾性。這就是著名的哥德爾不完備性定理。這個結果使希爾伯特方案成為不可能。但1936年，G.根岑降低了希爾伯特的要求，允許使用無窮長的證明，證明了算術公理系統的無矛盾性。到1960年，數學分析的一些片斷的無矛盾性也被證明。20世紀60年代以後，證明論不再局限於無矛盾性的證明。數學證明中的結構，證明的複雜性，數學中不可判定問題都成為證明論的研究課題，1977年，J.帕里斯發現算術理論中的一個自然的而又是不可判定的命題，這是一個重大發現。它使算術中自然的不可判定命題的研究越來越受人注意。

亞結構邏輯

在數理邏輯中，特別是聯合上證明論的時候，一些亞結構邏輯已經作為比常規系統弱的命題演算系統被介入了。同常規系統的不同之處在於它們有更少的結構規則可用：結構規則的概念是基於相繼式（sequent）表達，而不是自然演繹的公式化表達。兩個重要的亞結構邏輯是相干邏輯和線性邏輯。

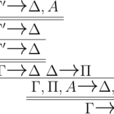
在相繼式演算中，你可以把證明的每一行寫為

這裡的結構規則是重寫相繼式左手端的Γ的規則，Γ是最初被構想為命題的字元串。這個字元串的標準解釋是合取式：我們希望把相繼式符號

讀做(A與B)蘊涵C。

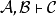
這裡我們把右手端的Σ採納為一個單一的命題C（這是直覺主義風格的相繼式）;但是所有的東西都同樣的適用於一般情況，因為所有的操作都發生在十字轉門（turnstile）符號的左邊。

因為合取是交換性和結合性的操作，相繼式理論的形式架設通常包括相應的結構規則來重寫相繼式的Γ - 例如

演繹自

還有對應於合取特性的冪等性和單調性的進一步的結構規則：從

我們可以演繹出

還有從

我們可以演繹出，對於任何B

在線性邏輯中有重複的假設（hypothese）'被認為'不同於單一的出現，它排除了這兩個規則。而相干邏輯只排除後者的規則，因為B明顯的與結論無關。

這些是結構規則的基本例子。在套用到常規命題演算的時候，這些規則是沒有任何爭議的。它們自然的出現於證明理論中，並在那裡被首次注意到（在獲得一個名字之前）。