萊斯利矩陣

萊斯利矩陣是科學家LesliePH.於1945年引進一種數學方法，利用某一初始時刻種群的年齡結構現狀，動態地預測種群年齡結構及數量隨時間的演變過程。

基本介紹

• 中文名：萊斯利矩陣
• 外文名：Leslie
• 提出者：LesliePH
• 提出時間：1945年
• 套用學科：生物科學

方法介紹

依種群個體的生理特徵,將其最大壽命年齡等距分成m個年齡組,然後討論不同時間種群按年齡的分布,故時間也離散化為t=0,1,2,…其間隔與年齡組的間隔時間相同.t=0對應於初始時刻.

設開始時(t=0)第i個年齡組內的個體數為ni(0),i=1,2,…,m.則向量

N∼(0)=[n1(0),n2(0),…,nm(0)]T稱為初始年齡結構向量.

第i年齡組的生殖率為fi(≥0)i=1,2,…,m;生存率為Si(>0),i=1,2,…,m-1.則相臨兩個時段間,各年齡組個體數ni有如下的疊代關係:

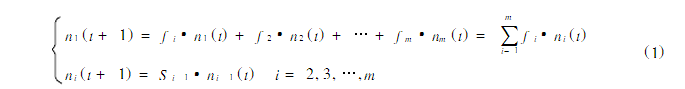
注1 fi中已扣除了在時段t內出生,但活不到t+1時段的新生個體.

注2 通常在兩性生殖的種群中,只計雌體數.作矩陣

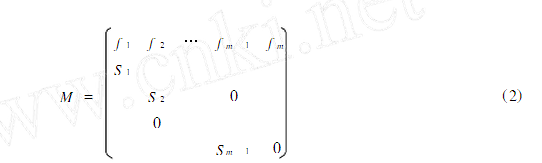
發展趨勢

利用萊斯利模型,對佛坪自然保護區內大熊貓種群的發展變化作出預測分析.

2.1 佛坪大熊貓種群現狀 佛坪自然保護區位於秦嶺中段南坡,北緯32°32′～33°43′,東經107°40′～107°55′,最高海拔2904m,最低海拔1100m,總面積293km2.1974年以來,科學工作者多次對該區域內大熊貓的種群數量、年齡結構、分布等進行了大量觀察研究,提供了如下數

據[3].1990年該區域內觀察到64隻大熊貓,分布面積237km2,密度為0.27󰃗km2,年齡結構為

未成年組 6歲以下 24隻 37.5%

成年組 6～15歲 31隻 48.2%老年組 15歲以上 9隻 14.3%

2.2 等距年齡結構分析處理 由於模型分析中要求等距年齡結構,現有的數據是不等距的,故需進行等距年齡結構分析處理.

根據大熊貓的生長發育規律,其野外最大壽命年齡為26歲[2],按每3歲一個年齡段分成9個年齡組:0歲～2歲,3歲～5歲,…,24歲～26歲,分別記為第1,2,…,9年齡組.

文[4]已據文[2]提供的大熊貓的有關生命數據,換算出大熊貓按三年段的等距年齡組的生殖率fi和生存率Si為表1.

由於野外大熊貓的性別不易識別,調查數據往往無性別之分,大熊貓的雌雄比為1∶1[2],故上表為雌、雄合計的,而非一般的只考慮雌體.

文[5]計算了大熊貓種群的穩定年齡結構向量為

N∼(∞)=[101,41,37,33,27,15,8,4,1]t

據此,可按比例將現有非等距年齡結構調整為等距年齡結構.0～5歲共24隻屬於第1、2年齡組.因0～2歲幼仔死亡率極高,加之9月以前的幼仔不能離窩,不可能見到它們的活動痕跡,故第一年齡組的個體數應增加,能被觀察到的個體數量以三分之一計算[3].於是n1󰃗3+n2=24;n1󰃗n2=101󰃗41,解得n1=33(只),n2=13(只).6歲至15歲31隻,但分齡到14歲,尚多出1歲,故調出1隻到下一組內,餘下的30隻仍按比例分配調整為n3=12隻,n4=11隻,n5=7隻.16歲以上9隻,調入一隻後共10隻,按比例分配調整為n6=4隻,n7=3隻,n8=2隻,n9

=1隻.最後得到1990年(t=0)的初始年齡結構向量為N∼(0)=[33,13,12,11,7,4,3,2,1]T.

萊斯利矩陣為

使用案例

對t=1,2,…,10,11,按公式N∼(t)=MtN∼(0)的計算結果見表2.其中

N∼(0)=[33,13,12,11,7,4,3,2,1]

T表2 佛坪大熊貓種群發展趨勢

從計算結果可以看到,自1990年起的33年間,該種群數量共增加30.39隻,為原來的1.353倍,增長率為35.3%.可見大熊貓的發展十分緩慢.不過,這一瀕危動物尚能緩慢增長也算幸事了.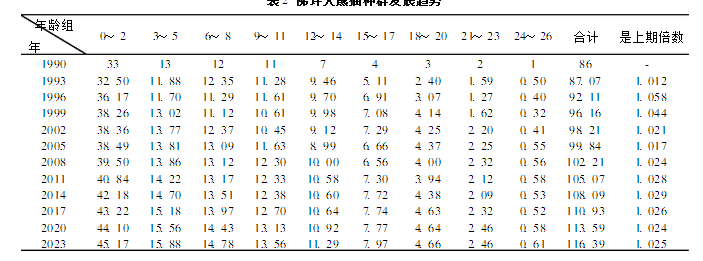

大熊貓種群發展趨勢

為分析環境對大熊貓的影響,即因環境造成大熊貓個體的非正常的突發性死亡(如捕

獵等).假設1990年內,第二、三、四、五年齡組分別有1隻大熊貓非正常死亡,即按N∼(0)=[33,12,11,10,6,4,3,2,1]T計算,以後33年間該大熊貓種群按年齡結構的發展見表3

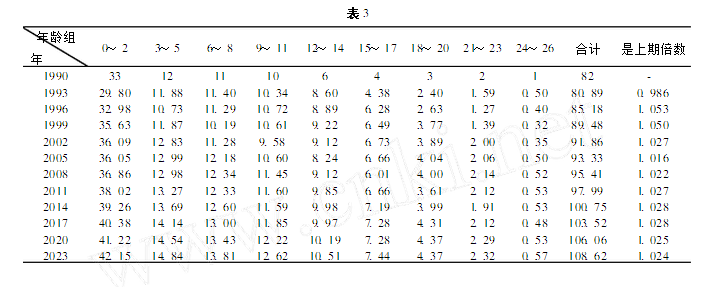大熊貓年齡結構

由表2與表3對照表明,雖少量個體受損對種群的影響也是顯著的,需經過近十年時間種群才能恢復到原有水平,而且對種群總量的影響還將長期持續下去,可見保護好大熊貓的生存環境,儘量杜絕和減少非正常死亡是十分重要的。