基本介紹
- 中文名:自適應選擇
- 外文名:Adaptive selection
- 涉及領域:信息科學
- 特點:自適應性
- 根據:信號等的不同
- 套用:自動化
自適應選擇
預測模型的自適應選擇
特性
模型自適應選擇方法
背景分析
模型方法庫
建立判別理論基礎
- 第一項是偏差平方,它反應了由於真正偏差引起的預測誤差;
- 第二項是以斜率餘數平方和做權數引起的預測誤差,它反應了斜率的誤差;
- 第三項是以實際值與預測判別係數的餘數為權數的實際方差,它反應了誤差中有殘差部分。
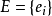



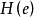
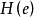



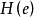
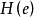
自適應選擇(Adaptive selection)是指根據信號的不同自適應的對條件進行選擇。自適應是在處理和分析過程中,根據處理數據的數據特徵自動調整處理方法、處理順序、處理...
自適應就是在處理和分析過程中,根據處理數據的數據特徵自動調整處理方法、處理順序、處理參數、邊界條件或約束條件,使其與所處理數據的統計分布特徵、結構特徵相適應,...
適應性選擇指自然界中的生物為了生存和競爭在逐漸變化的生存環境中適應並生存,這種由外界環境變化未帶來的物種的變化成為生物的適應性選擇。...
自適應遺傳算法(Adaptive Genetic Algorithm,AGA)是對基本遺傳算法的一種改進,它通過對遺傳參數的自適應調整,大大提高了遺傳算法的收斂精度,加快了收斂速度。...
自適應選擇明文攻擊(adaptive-chosen-plaintext attack):是選擇明文攻擊的一種特殊情況,指的是密碼分析者不僅能夠選擇被加密的明文,也能夠依據以前加密的結果對這個...
自適應最優控制(Adaptive optimal control )是指根據控制對象本身參數或周圍環境的變化,自動調整控制器參數以使控制系統的性能指標實現最最佳化的基本條件和綜合方法,...
自適應能力一般是指系統按照環境的變化,調整其自身使得其行為在新的或者已經改變了的環境下達到最好的或者至少是容許的特性和功能所具有的能力。...
速率自適應,即在通信系統中,根據當前信道實時狀態,改變傳送數據速率,以提高系統傳輸性能。速率自適應的速率選擇算法核心是及時獲取能夠實時反映信道狀態的信息。...
自適應通信(adaptive communication),是指具有自動適應通信條件變化能力的無線電通信。主要的自適應通信技術有:實時自動選頻、通信頻率自動跳變、自適應調零天線陣、...
自適應( self-adaptive)是指處理和分析過程中,根據處理數據的數據特徵自動調整處理方法、處理順序、處理參數、邊界條件或約束條件,使其與所處理數據的統計分布特徵、...
自適應控制技術套用 自適應控制技術套用 2、無模型自適應控制方案實施 ⑴控制器選擇CyboCon CE。該控制器是美國博軟公司將無模型自適應(MFA)控制技術與Microsoft ...
自適應控制作用是指機器人依據周圍環境所獲得的信息來修正對自身的控制,這種控制器配有觸覺、力覺、接近覺、聽覺和視覺等感測器,能夠在不完全確定或局部變化的環境...
互連網路路由器是大規模並行處理機系統的關鍵部件,根據其所採用的路由算法可分為確定性和自適應路由器兩種,自適應路由器對於一對源和目的結點,視網路的工作狀態,可...
自適應調度是指在滿足不同工作方式相對優先權的條件下,在設計範圍內,同時實時地平衡各種波束請求所要求的時間、能量和計算機資源,為一個調度間隔選擇一個最佳任務...
自適應邏輯(adaptive logic,簡稱AL)並不是通常意義上的邏輯系統,而是一個形式化的證明框架。自適應邏輯的主要特點是它能夠靈活地適應具體的前提集合,根據特定的異常...
自適應稀疏表示(Adaptive sparse representation)由信號的自適應稀疏表示和原子庫的更新疊代實現原子庫的訓練。信號稀疏表示的目的就是在給定的超完備字典中用儘可能少...
自適應構件是跟隨建築信息模型(BIM)概念而產生的理念,作為某些特性參數可變的部件,貫穿於整個設計項目的CAD和CAE過程。...
自適應控制,指的是根據控制對象本身參數或周圍環境的變化,自動調整控制器參數以獲得滿意性能的自動控制方法。預測控制是近年來發展起來的一類新型的計算機控制算法。...
自適應補償(Adaptive compensation)是根據系統執行器的冗餘情況,設計自適應補償控制律,利用有效的執行器,達到跟蹤參考模型運動的控制目的,同時保持較好的動態和穩態性能...
自適應調製編碼是AMC技術,用戶數據傳送可以採用高階調製和高速率的信道編碼方式。...... AMC是根據無線信道變化選擇合適的調製和編碼方式,網路側根據用戶瞬時信道質量...
為提高通信系統的穩定和可靠性,根據線性數字的調製信號的特點,對數位訊號進行非線性變換,套用變換後信號的功率譜密度中所包含的信號特徵信息,提出了一種適合於自適應...
計算機自適應測驗(Computerized Adaptive Testing,簡稱CAT)是近年來發展起來的一種新的測驗形式。這種測驗以項目反應理論為基礎,以計算機技術為手段,在題庫建設、選題...
自適應調製與編碼簡稱為AMC(Adaptive Modulation and Coding),是一種基於物理層的鏈路自適應技術。AMC技術的基本原理是在傳送功率恆定的情況下,通過調整無線鏈路傳輸...
可以採用固定規律的調節器,假若變化大,質量要求又高時,需要選擇可變規律調節器。...對象訊識別和調節器的規律的計算都用一個計算裝置進行,就叫自適應自整定調節,...
執行器故障自適應補償控制是根據系統執行器的冗餘情況,設計自適應補償控制律,利用有效的執行器,達到跟蹤參考模型運動的控制目的,同時保持較好的動態和穩態性能的控制...
