基本介紹
- 中文名:聯立模組法
- 外文名:two tier approach
- 又稱:雙層法
- 學科分類:化學
基本思想
發展概況


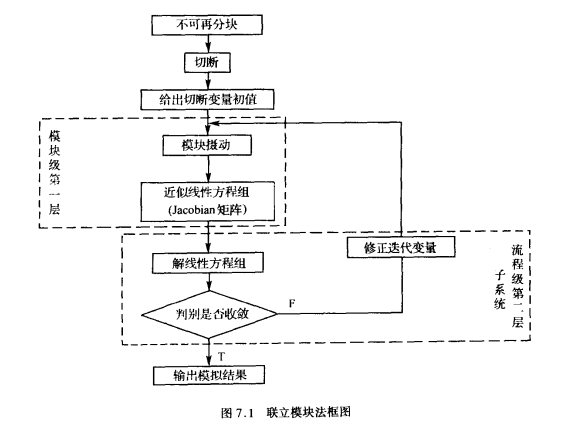
聯立模組法結構分析的特點
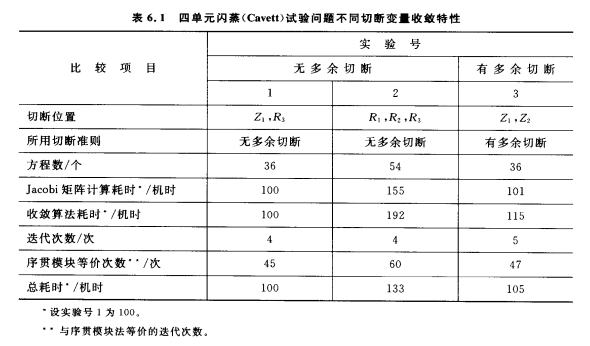
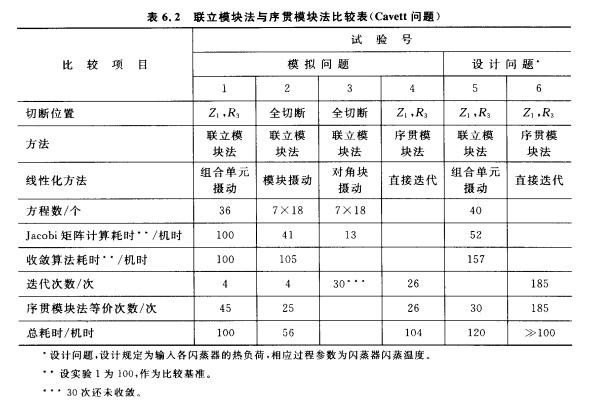
聯立模組法與序貫模組法的比較





聯立模組法,就是指既充分利用了現有的常規模組,又進行方程組的聯立求解的一種流程模擬方法,它也被稱作雙層法。基本思想1、繼承序貫模組法的模組化的結構,充分利用現有的豐富成熟的單元模組的成果。2、僅對分隔後的不可再分塊使用聯...
全書共分11章,內容包括緒論、過程系統的穩態模擬、序貫模組法、聯立方程法、聯立模組法、最最佳化方法、換熱網路綜合、能量集成、分離序列綜合、質量集成、水系統集成。 《化工過程分析與綜合(第二版)》是作者在總結多年教學和科學研究實踐的基礎上,吸收了近年來本學科領域在過程綜合集成與最佳化方面的理論研究與套用成果...
《化工過程分析與綜合》是2010年化學工業出版社出版的一本圖書,作者是鄢烈祥。內容簡介 本書論述了化工過程系統模擬與分析、綜合與集成和最最佳化的基本理論和方法。全書共12章,內容包括:緒論、過程系統模型及其求解方法、序貫模組法、聯立方程法、聯立模組法、流程模擬系統簡介、最最佳化方法、換熱網路綜合、能量集成、...
gPROMS(general PROcess Modelling System)採用聯立模組法,解決了上述問題。gPROMS是帝國理工學院(Imperial College London)PSE(Process System Enterprise Ltd.)研究中心在多年建模和仿真實踐中的研究成果。gPROMS的研發始於1988年,是由曾經開發SPEEDUP(現歸入Aspen的ACM模組)的研究人員完成的,1992年開始進行工業評估,5年...
2.5.1 聯立模組法的原理 2.5.2 建立簡化模型的兩種切斷方式 2.6 氨合成工藝流程的模擬與分析 2.6.1 氨合成工藝流程的模擬 2.6.2 氨合成工藝生產工況的模擬分析 2.7 過程系統穩態模擬軟體 2.7.1 ASPEN 2.7.2 PRO/Ⅱ 參考文獻 第三章 化工過程系統動態模擬與分析 3.1 化工過程系統的動態模型 3.1...
第三節 過程系統模型的聯立方程法求解 一、聯立方程法的基本思想及其特點 二、方程組的分隔和切斷 三、聯立方程組的解法 第四節 過程系統模型的聯立模組法求解 一、聯立模組法的基本特點――多個流程模型 二、聯立模組法對四種疊代的處理 三、二層法 第五節 流程模擬的計算機輔助技術 一、化工模擬系統的分類 二...
本課題以聯合循環進氣冷卻總能系統的全工況動態最佳化控制特性為研究對象;在提出新的最佳化目標函式與評價準則的基礎上,建立基於模型預測的聯立模組法動態最佳化控制模型,並進行仿真。在關鍵問題上提出創新性的解決方案,並套用於聯合循環電站進氣冷卻系統的設計、性能預測、故障診斷和運行最佳化控制,以達到節能降耗的目的。
9.2序貫模組法 9.3聯立方程法 9.4聯立模組法 9.5模擬方法比較 9.6分離過程模擬 參考文獻 習題 第10章分離過程系統合成 10.1分離系統的組織 10.2試探合成 10.3調優法合成 10.4最最佳化合成 參考文獻 習題 第11章分離過程的能耗及節能措施 11.1分離過程所需理論最小功 11.2分離過程的節能措施 ...
第1章緒論,介紹過程系統工程的發展歷史、研究內容、套用範圍以及化工過程系統工程的基本概念;第2章單元過程及其模組,介紹單元過程的數學模型及單元自由度;第3章過程系統的結構分析,介紹系統結構模型及其分解方法;第4~6章,分別介紹過程系統模擬的三種主要方法:序貫模組法、聯立方程法和聯立模組法;第7章過程系統...
2.3 過程系統模擬的聯立方程法 2.3.1 大型稀疏非線性方程組的降維解法 2.3.2 聯立線性方程組法解大型稀疏非線性方程組 2.4 過程系統模擬的聯立模組法 2.4.1 簡化模型的建立方法 2.4.2 攝動法求簡化模型係數矩陣 2.5 過程模擬的套用 2.5.1 氨合成工段的流程 2.5.2 氨合成工段的穩態模型 2.5....
本書著重介紹過程系統工程的基礎知識和主要方法。圖書目錄 目錄 第一章 緒論 第二章 化工過程系統數學模擬方法 第三章 過程系統的分解 第四章 非線性代數方程組解法 第五章 序貫模組法 第六章 聯立方程法 第七章 聯立模組法 第八章 過程系統的最最佳化 第九章 其他最佳化問題簡介 第十章 過程系統的合成 習題 ...
2.2.2 聯立方程法 2.2.3 聯立模組法 本章符號說明 參考文獻 習題 第3章 過程系統自由度分析及系統分解 3.1 自由度分析 3.1.1 單元過程自由度分析 3.1.2 過程系統的自由度分析 3.2 化工過程系統的分解 3.2.1 問題的提出 3.2.2 不相關子系統的識別 3.2.3 對不相關子系統的...
不可行路徑法 每一次疊代都不是從一個可行點開始,僅在最後達到最優解時,計算結果才表示為一個可行點的最佳化方法。infeasible path method 這種方法搜尋路徑的中間點沒有具體的物理意義,它可大大。不可行路徑法可用於,包括序貫模組法、聯立模組法、聯立方程法等。
24過程系統模擬的面向方程法29 241面向方程法的原理29 242大型稀疏非線性方程組的降維解法30 243聯立擬線性方程組法解大型稀疏非線性方程組34 25過程系統模擬的聯立模組法39 251聯立模組法的原理39 252建立簡化模型的兩種切斷方式41 26氨合成工藝流程的模擬與分析45 261...
3.4.2 聯立方程法 3.4.3 聯立模組法 3.5 過程系統模擬的基本步驟 3.6 化工過程穩態模擬軟體介紹 3.7 過程系統模擬的套用實例 本章符號說明 參考文獻 習題 第4章 夾點技術的基礎理論 4.1 過程系統的夾點及其意義 4.1.1 溫一焓圖 4.1.2 組合曲線 4.1.3 在T-H圖上描述夾點 4.1.4 用“問題表格...
43聯立方程法與聯立模組法 119 44動態流程模擬系統 124 441動態模擬的特點124 442動態模擬的數學描述125 443動態序貫模組法126 45化工裝置仿真機 127 451系統構成128 452關鍵技術129 453套用領域129 本章要點130 思考題4130 本章參考文獻130 第5章運籌學方法 51...
3.5聯立方程法(51)3.5.1聯立方程法的基本問題(51)3.5.2方程組的分隔(53)3.5.3不可分隔方程組的斷裂(56)3.5.4稀疏線性方程組的分解(59)3.5.5聯立方程法的優缺點(62)3.6聯立模組法(62)3.6.1簡化模型的建立方法(63)3.6.2聯立方程法的特點(64)3.7化工過程模擬軟體簡介及其套用(65)3.7.1...
3.4聯立方程法103 3.4.1聯立方程法的基本思想103 3.4.2流程系統方程組的產生103 3.4.3聯立方程法的求解策略104 3.4.4方程組分解106 3.4.5稀疏線性方程組求解107 3.4.6聯立方程法的優缺點108 3.5流程模擬的其他方法109 3.5.1聯立模組法109 3.5.2數據驅動法109 3.5.3人工智慧參入法109 3.6...
33聯立方程法118 34聯立模組法119 35化工系統的分解122 351系統分隔123 352系統的切斷126 36設計(獨立)變數的選擇130 361問題的提出130 362拓撲雙層圖131 37大型方程組的分解策略133 371指定方程組每一方程的輸出 變數135 372利用方程組輸出變數集,繪製方程 ...
1.3基於聯立方程法的過程模擬22 1.3.1大型稀疏非線性方程組的降維解法23 1.3.2大型稀疏非線性方程組的聯立線性方程組解法25 1.4基於聯立模組法的過程模擬26 1.4.1簡化模型的建立方法27 1.4.2攝動法求簡化模型係數矩陣30 習題31 第2章化工過程動態模擬與控制/33 2.1基本概念33 2.2動態數學模型37 2.2...
