基本介紹
- 中文名:耳分解
- 外文名:Ear Decomposition
- 所屬學科:圖論
定義
中文定義
英文定義




性質
充分性









必要性


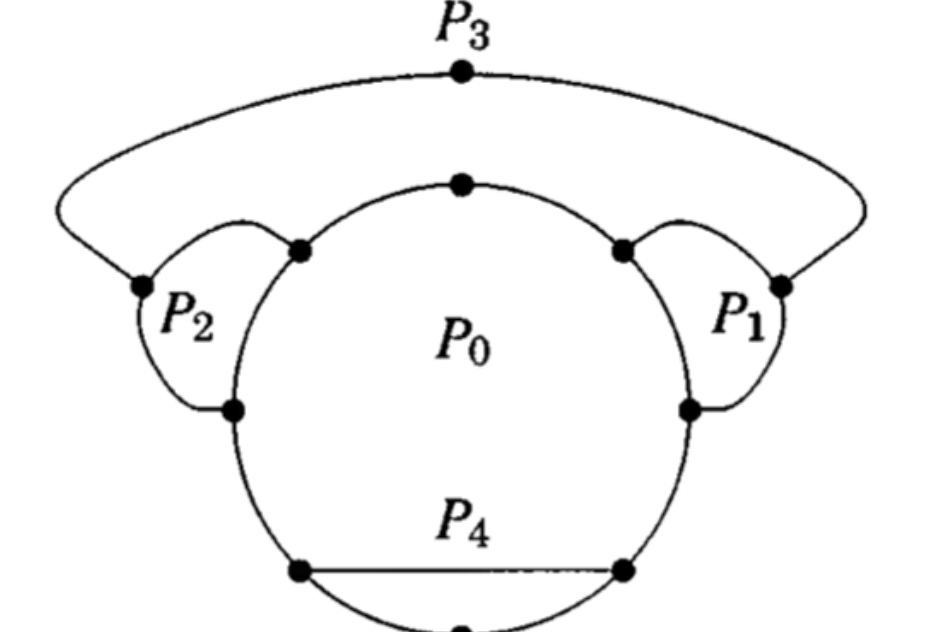















耳分解是一種對圖的分解方法。圖論中耳的定義就是一條極大的路徑,路徑內部(不包括端點)的度均為2。耳分解就是將圖分解為一個環和若干個耳。定義中文定義耳指的是內部點度數均為2的極大路徑。耳分解指的是將圖分解為一個環和若干個耳...
或幼果)異常生長,開成茶耳(茶泡).這種生長有點類似動物的"腫瘤",會分解本射的一些纖維素,變為糖,所以吃起來有點甜,但這些變態的東西生命不會很長的.清明前後長勢最好,此時茶油果子,樹葉都剛屬幼齡,容易發生異變;另外茶樹被砍後,來年生長出來的新茬產出的幼葉最多,變異成茶耳的幾率也是最多的。
第六節耳甲艇部分 第七節三角窩部分 第八節耳舟部分 第九節對耳輪部分 第十節對耳輪上、下腳部分 第十一節耳輪及耳輪腳部分 第十二節耳背部分 第五章耳穴的功能 第一節新增耳穴的特定功能 第二節耳穴的功能歸類 第六章耳穴的刺激方法 第一節手法按摩 第二節貼敷法 第三節針刺與放血 第四節提高療效的環節...
《圖解頭耳簡易按摩》是由哈爾濱出版社於2010年出版的一本書籍,作者王濤叢。內容簡介 《圖解頭耳簡易按摩》將按摩的部位細分到頭耳部分,圖文並茂、內容詳細、通俗易懂。書中附帶了頭部穴位分布圖與耳部分解圖,通過《圖解頭耳簡易按摩》可以讓您了解頭耳部的幾種常用按摩手法、操作要領與主治病症,同時還詳盡介紹了...
《圖解耳壓療法》是2007年5月人民軍醫出版社出版的圖書,作者是吳杞、歐陽欣。本書講述了常見病症的耳穴貼壓療法治療。內容簡介 本書共分5章,以要點形式扼要介紹了常見病症在耳廓上的病理性反應和對症取穴,以及有關耳穴貼壓療法的手法與腧穴定位技巧;重點介紹了常見病症的耳穴貼壓療法治療,並配以大量的步驟分解...
流耳,耳狀食用菌類栽培病害之一,是因細胞破裂流水的一種生理障礙現象,指黑木耳、銀耳等子實體組織破裂、分解變軟,水腫糜爛,向外流滲黏性膠液,造成嚴重減產。從致病原因上看,流耳分為生理性流耳、微生物病原性流耳、蟲害致病流耳。致病原因 根據致病原因,流耳分為生理性流耳、微生物病原性流耳、蟲害致病...
實驗結果顯示,採用聯合因子分析(JFA)的方法將耳語音的特徵分解為說話人空間、信道空間和殘差空間三個部分,並形成由說話人超向量和信道超向量等組成超向量,JFA的方法可提高不匹配信道下耳語說話人的識別率;在短時語音測試時用混合補償法可提升約3%的識別率;正弦模型及人耳聽覺模型的全局譜參數可將耳語說話人狀態...
銀耳絕大多數種類都生於各種樹木的原木上。但銀耳菌絲幾乎沒有分解纖維素的能力,因此在其完成生活史的過程必須依賴另一種真菌的協助即香灰菌,又稱耳友菌,亦稱羽毛狀菌絲,它能把銀耳菌絲無法利用的纖維素、木質素、澱粉等分解為銀耳菌絲可以吸收的營養成分。溫度 銀耳屬中溫性真菌,銀耳培養過程離不開伴生菌絲香灰...
耳穴刺針減肥法:加速脂肪分解快速瘦身。耳廓的神經、血管最為豐富,刺激耳甲廓、耳甲腔等處,有調整機體內分泌系統以及內臟功能的作用,尤其是刺激迷走神經可影響胰島素值,進而掏食慾,達到減肥的目的。具體方法 1、找準穴位:將局部進行常規消毒,進針的時候左手要固定耳廓,右手要以半寸或1寸3號毫針垂直的刺入...
久之其中心腐敗、分解、變性,產生膽固醇結晶。外耳道膽脂瘤可並發膽脂瘤型中耳乳突炎,也可引起周圍性面癱。膽脂瘤型中耳炎與慢性顯著化膿性中耳炎有密切的關係經常。中耳發炎長期流膿,鼓膜受膿液腐蝕,穿孔,多次外耳道表皮易沿穿孔進入中耳腔及乳突腔。其上皮層角化,反覆脫落、積累、壓迫周圍骨質,使之吸收形成空腔。
2.新黴素、卡那黴素等即使停用,在體內也已完全分解、排泄,但由藥物引起的內耳毛細胞的退化及聽神經細胞的變性萎縮卻仍在繼續進行,直至聽力完全喪失變為全聾,此稱“漸進性耳毒反應”。3.耳毒性抗生素包括鏈黴素、雙氫鏈黴素、卡那黴素、慶大黴素、多黏菌素、萬古黴素、春雷黴素等。它們都是廣譜抗生素,在化學...
1. 鮮木耳含有一種卟啉的光感物質,人食用後經太陽照射可引起皮膚瘙癢、水腫,嚴重的可致皮膚壞死。乾木耳是經暴曬處理的成品,在暴曬過程中會分解大部分卟啉,而在食用前,乾木耳又經水浸泡,其中含有的剩餘卟啉會溶於水,因而水發的乾木耳可安全食用;2. 優質木耳表面黑而光潤,有一面呈灰色,手摸上去感覺乾燥,無...
和模擬記錄的方式不一樣,數位化記錄聲音必須將連續的聲音波形分解成一個個離散的點並用數字的方式記錄,如圖1所示,這就是採樣。聲音採樣 為什麼用採集的離散的點就可以還原聲音,這其實利用了人耳的生理特性。為了更好的理解,舉一個例子,卡通片是將無數張靜態的畫面連在一起播放,這其實利用了人眼的生理特性,...
穆稜黑木耳色澤純正,背面少筋脈,形狀為碗狀或茶葉狀。耳質耐水性強,經水浸泡一周后,耳質不分解,色澤仍光亮新鮮,耳質肥厚,味道鮮美,香味濃厚,品質極佳。內在品質指標 穆稜黑木耳營養豐富,胺基酸總量≥8%,粗蛋白質含量≥9%,粗脂肪小於2%,粗纖維含量≥4%,總糖含量≥28%,鈣含量≥490毫克/100克,鐵...
中耳膽固醇肉芽腫,膽固醇肉芽腫是一種含有膽固醇結晶和多核巨細胞的肉芽腫,發生於鼓竇、乳突或鼓室內者,稱中耳膽固醇肉芽腫。分類 疾病 病理病因 膽固醇肉芽腫屬非特異性病變,是組織對膽固醇結晶產生的異物反應。如因各種原因引起中耳出血、血漿滲出、組織水腫、組織壞死等,以致紅細胞破裂、分解,脂肪發生退行性變,...
藥線作為一種異體蛋白,埋入穴位以後相當於異種組織移植,可使人體產生變態反應,使淋巴細胞致敏,其細胞又配合體液中的抗體,巨噬細胞等,反過來破壞分解、液化藥線,使之變成多肽、胺基酸等,最後被吞噬吸收,同時產生多種淋巴因子。這些抗原刺激物對穴位產生生理物理及生物化學刺激,使局部組織產生變態反應和無菌性炎症...
消化不良、高脂血症及慢性胃炎等症又常需要二者配合套用。2、本穴可使胃酸分泌增加,胃酸分泌多者禁用;還有抗脂肪分解的作用,能增強脂肪細胞攝取血中脂肪酸和抑制體內脂肪分解,減少血中的游離脂肪酸;還可治療偏頭痛、瘧疾。相關論述 《針灸穴位掛圖說明》:“胰膽 在十二指腸穴的上方,左耳為胰,右耳為膽。”
蘿北黑木耳,黑龍江省蘿北縣特產,全國農產品地理標誌。 蘿北黑木耳色澤純正,背面少筋脈,形狀為碗狀或茶葉狀。耳質耐水性強,經水浸泡一周后,耳質不分解,色澤仍光亮新鮮,耳質肥厚,味道鮮美,香味濃厚。2015年11月05日,原中華人民共和國農業部批准對“蘿北黑木耳”實施國家農產品地理標誌登記保護。產品特點 ...
茶樹換新葉時雨水特別多,而且這時茶果也還很小,由營養過剩引起的異常生長,開成茶耳(茶苞)。會分解本身的一些纖維素,變為糖,所以吃起來有點甜,但這些東西生命不會很長。防治措施 由於茶耳對茶樹的危害,往往會造成茶樹大面積減產,茶農一般視其為重點病害。在此概念的基礎上簡單敘述其防治措施:防治上需從...
鮮木耳含有一種卟啉的光感物質,人食用後經太陽照射可引起皮膚瘙癢、水腫,嚴重的可致皮膚壞死。乾木耳是經暴曬處理的成品,在暴曬過程中會分解大部分卟啉,而在食用前,乾木耳又經水浸泡,其中含有的剩餘卟啉會溶於水,因而水發的乾木耳可安全食用;優質木耳表面黑而光潤,有一面呈灰色,手摸上去感覺乾燥,無顆粒感...
使皮膚暴露部分出現紅腫、癢痛,產生皮疹、水泡,水腫。相比起來,乾木耳更安全。因為乾木耳是新鮮木耳經過曝曬處理的,在曝曬過程中大部分卟啉會被分解掉。食用前乾木耳又要用水浸泡,這會將剩餘的毒素溶於水,使乾木耳最終無毒,但要注意的是,浸泡乾木耳時最好換兩到三遍水,才能最大程度析走有害物質。
木耳中的多糖體能分解腫瘤,所以能提高人的免疫力,具有很好的抗癌作用。而這種多糖體也具有疏通血管、清除血管中膽固醇的作用,所以可以降血糖、降血脂、防止血栓形成,預防腦血管疾病發生。木耳中的了磷脂質,對腦細胞有營養作用,因此木耳是很好的補腦食品。木耳還具有滋補潤燥、養血益胃的食療效果,所以是各種現代文明...
