基本介紹
- 中文名:耦合模理論
- 外文名:coupled-mode theory
- 說明:多個電磁波模式間耦合的一般規律
- 補充:發生在不同類型的波動之間
詳述,發展概況,耦合模方程,弱耦合情況,強耦合情況,耦合功率理論,
詳述
研究兩個或多個電磁波模式間耦合的一般規律的理論,又稱耦合波理論。廣義地說,它是研究兩個或多個波動之間耦合的普遍理論。耦合可以發生在同一波導(或腔體)中不同的電磁波模式之間,也可以發生在不同波導(或腔體)的電磁波模式之間。通常,耦合發生在同一類波動之間,但也可以發生在不同類型的波動之間,例如行波管中的兩個電磁波模式與兩個空間電荷模式之間的耦合。
發展概況
J.R.皮爾斯在40年代研究微波電子管時首先提出耦合模概念,隨後S.E.米勒和S.A.謝昆諾夫發展了這一概念,並初步建立了波導模式耦合的基本理論。在50~60年代,耦合模理論已成功地用於分析參量放大器、多模圓波導傳輸和各嚮導性媒質填充波導等問題,中國科學家黃宏嘉提出耦合本地簡正模的廣義理論,深化了耦合模概念並簡化了分析方法。70年代以來,耦合模理論又成功地套用於光波導問題,對光纖通信和光纖感測有重要的實際意義。
耦合模方程
 (1)
(1)式中Ai為耦合系統中第i個模的幅度;在耦合傳輸線問題中Kij=jβi,在耦合振盪問題中Kij=jωi,βi和ωi分別為模式i的相移常數和振盪頻率;Kij(i厵j)為耦合係數,在傳輸線問題中是空間坐標z的函式,在振盪問題中是時間t的函式,是單位耦合長度或單位時間內由單位幅度的模j所激發的模i的幅度。將方程組 (1)寫成矩陣形式
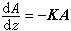 (1a)
(1a)式中A為列矩陣,k為耦合係數方陣。
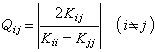 (2)
(2)弱耦合情況
指任何i、j(i厵j)都符合條件
Qij1 (3)
A1(0)=1 Ai(0)=0 (i厵1) (4)
則在z=L處的近似解為
 (5)
(5)可見,即使存在多個模之間的耦合,仍可以分別考慮每一個模與輸入模之間的耦合,從而使問題簡化。
強耦合情況
通常,強耦合只發生在兩個耦合模式(如1和2)之間,忽略其他耦合模,可將式(1)簡化為
 (6)
(6)設只有模式1輸入耦合系統,且β1=β2=β(即Q12→∞)和K12=K21=-jc都是常數,則式(6)的解為
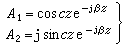 (7)
(7)圖1給出|A1|和|A2|隨坐標z的變化的曲線,其中實線表示β1=β2情況下的解式(7),說明兩種模式之間可以實現能量的完全轉換;虛線表示常耦合和β1厵β2情況下的解,可見,這時不可能實現能量的完全轉換。 圖1
圖1
 圖1
圖1在周期性耦合情況下,耦合能力為
 (8)
(8)適當選擇周期λ1,即使在Kii厵Kjj的情況下也可能使(右圖)實現模式間能量的完全轉換。


 圖2
圖2