基本介紹
- 中文名:羅姆方
- 外文名:Room square
- 所屬學科:數學(組合學)
- 簡介:一類特殊的組合設計
基本介紹
a | b | c | d | e | f | g |
35 | 17 | ∞2 | 46 | |||
26 | ∞4 | 45 | 37 | |||
13 | 57 | ∞6 | 24 | |||
47 | 16 | ∞3 | 25 | |||
∞5 | 23 | 14 | 67 | |||
12 | ∞7 | 56 | 34 | |||
36 | 45 | 27 | ∞1 |
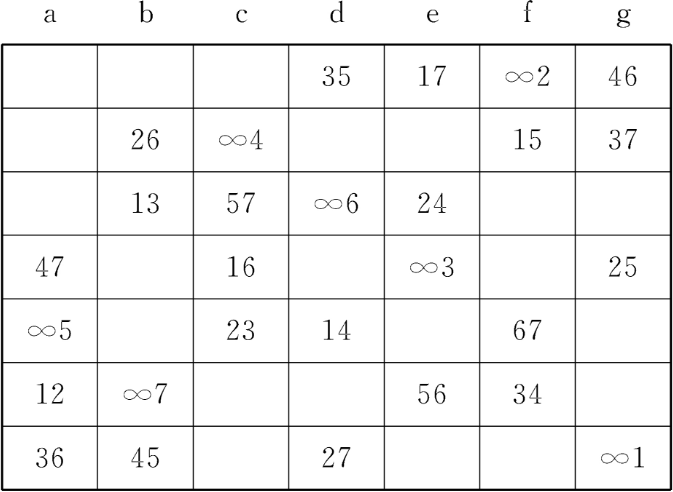
a | b | c | d | e | f | g |
35 | 17 | ∞2 | 46 | |||
26 | ∞4 | 45 | 37 | |||
13 | 57 | ∞6 | 24 | |||
47 | 16 | ∞3 | 25 | |||
∞5 | 23 | 14 | 67 | |||
12 | ∞7 | 56 | 34 | |||
36 | 45 | 27 | ∞1 |
羅姆方(Room square)是一類特殊的組合設計,將一個2n元集的所有2元子集放在一個2n-1階的方陣中,使其中每個位置或者空著,或者放一個2元子集,並使這2n個元在...
標準羅姆方(standardized Room square)特殊形式的羅姆方.設n階羅姆方的元素集合為{00 ,1, 2, w,n},若主對角線上元素對依次為{二,1},{二,2},…,{二,n...
完美羅姆方(perfect Room square)一類特殊的羅姆方.若完全圖Kz,的某個1因子分解中每兩個1因子的並是一個長2n的圈,則稱這樣的分解為完美1因子分解.若一個羅姆...
平衡羅姆方(balanced Room square)一類特殊的羅姆方.若將一個羅姆方的每個2元子集{二,少用有序對(二,y)或(y,二)代替,則所得的方陣稱為有序羅姆方...
羅姆子方(Room subsquare)特殊的羅姆方,即含於某羅姆方中的羅姆方.若一個廠階羅姆方的某、行及某、列的交叉位置上的、階方陣也構成某個、+1元集上的、階...
斜羅姆方(skew Room square)一類特殊的羅姆方.在一個標準羅姆方中,若關於主對角線對稱的每兩個位置中恰有一個是空的,則稱之為斜羅姆方.rt階斜羅姆方存在的...
t維羅姆方(t-dimensional Room square)羅姆方的高維推廣.設n階t維方陣中每個位置或者放一個元素的無序對或者空著,若它的每一個2維投影是一個n階羅姆方,則...
柯克曼方(Kirkman square),羅姆方的一種推廣。...... 柯克曼方(Kirkman square),羅姆方的一種推廣。.若V為v元集,F為一個方陣,其每個位置或者放一個V的k元...
正交對稱拉T方是一類組合對象...... 正交對稱拉T方(orthogonal-symmetric Latinsquare)一類組合對象.與羅姆方等價.設L=(l;;)及M= (m;;)是兩個n階的冪等對稱...
正交施泰納三元系(orthogonal Steiner triple system)是一類組合對象,是與羅姆方有關的對象。羅姆方也與正交施泰納三元系密切相關,由|X|=n時正交施泰納三元系的...
豪韋爾(Howell , E. C.)於1897年發現橋牌比賽安排問題也涉及到這一類方陣.羅姆(Room, T.G.)不知這些情況,於1955年提出這一類方陣的存在性問題,後來這類方陣...
