總體回歸函式表明被解釋變數Y的平均狀態(總體條件期望)隨解釋變數X變化的規律。至於具體的函式形式,是由所考察總體固有的特徵來決定的。
基本介紹
- 中文名:總體回歸函式
- 外文名:population regression function(PRF)
- 所屬領域:數學
- 相關概念:總體回歸線、線性回歸、回歸係數
定義










方程形式與套用













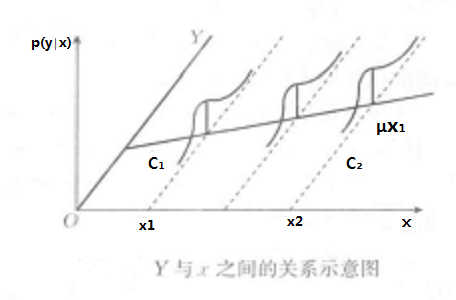

總體回歸函式表明被解釋變數Y的平均狀態(總體條件期望)隨解釋變數X變化的規律。至於具體的函式形式,是由所考察總體固有的特徵來決定的。
























總體回歸函式表明被解釋變數Y的平均狀態(總體條件期望)隨解釋變數X變化的規律。至於具體的函式形式,是由所考察總體固有的特徵來決定的。...
其中k為解釋變數的數目,βj(j=1,2,…,k)稱為回歸係數(regression coefficient)。上式也被稱為總體回歸函式的隨機表達式。它的非隨機表達式為...
為了保證多元回歸分析的參數估計、統計檢驗以及置信區間估計的有效性,與一元線性...式(2)稱為總體回歸方程(Population Regression Equation,PRE )或總體回歸函式(...
回歸分析就是要找出一個數學模型Y=f(X),使得從X估計Y可以用一個函式式去...是總體回歸係數,也是總體回歸直線的斜率。由式(2)不難理解,總體回歸方程描述的...
2.2.2 相關分析與回歸分析2.3 總體回歸函式2.3.1 總體回歸函式(PRF)2.3.2 總體回歸函式的形式2.3.3 總體回歸模型2.4 樣本回歸函式...
同方差性是經典線性回歸的重要假定之一,指總體回歸函式中的隨機誤差項(干擾項)在解釋變數條件下具有不變的方差。計量經濟學中, 一組隨機變數具備同方差即指線性...
作者遵循國際主流教材的思想,以套用為導向,深入淺出地介紹了計量經濟學理論及其在經濟實踐中的套用,涉及簡單回歸、多元回歸、模型函式形式、虛擬變數、模型診斷及模型...
10 回歸分析 10.1 回歸分析方法 10.1.1 回歸分析 10.1.2 相關關係、函式關係與回歸分析 10.1.3 回歸模型的建立 10.2 總體回歸、樣本回歸和誤差項...
異方差性是相對於同方差而言的。所謂同方差,是為了保證回歸參數估計量具有良好的統計性質,經典線性回歸模型的一個重要假定:總體回歸函式中的隨機誤差項滿足同方差性,...
偽隨機數函式(Pseudo random function) [1] 總體回歸函式(Population regression function)計量經濟學用語。 催乳素釋放因子(Prolactin releasing factor)【醫】 PRF ...
一、回歸與相關二、總體回歸函式三、隨機擾動項四、樣本回歸函式第二節 簡單線性回歸模型的最小二乘估計一、簡單線性回歸模型的基本假定...
第一節 一元線性回歸模型 第二節 一元線性回歸的基本概念 一、散點圖 二、總體回歸函式 三、隨機干擾項 四、樣本回歸函式 第三節 一元線性回歸模型的參數估計...
