線秩(line rank)是矩陣的一個指標,設A是(0,1)矩陣,A的行與列統稱為線,包含A的全部1的最小線數稱為A的線秩,柯尼希定理斷言:矩陣的線秩等於項秩,另外,矩陣的線秩等於該矩陣的具有非零積和式的子方陣的最大階數,亦等於矩陣經行或列的置換,具有全1主對角線的子方陣的最大階數。
基本介紹
- 中文名:線秩
- 外文名:line rank
- 所屬學科:數學(矩陣論)
- 簡介:矩陣的一個指標
- 別稱:覆蓋數
基本概念
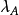
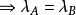
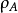

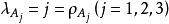
相關性質定理
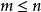





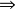





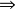
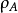










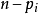
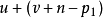

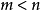
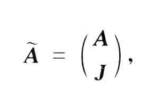


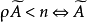
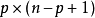



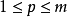

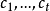






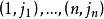


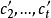
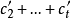





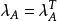





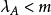
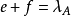
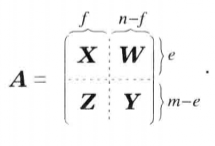
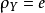
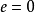
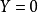

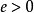
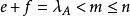
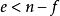




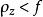
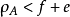

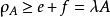
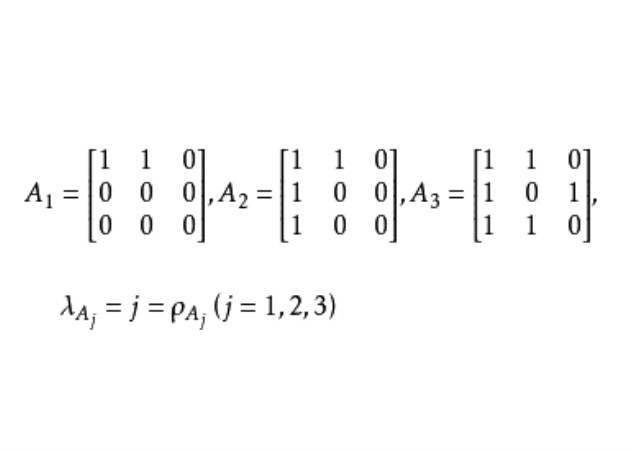
線秩(line rank)是矩陣的一個指標,設A是(0,1)矩陣,A的行與列統稱為線,包含A的全部1的最小線數稱為A的線秩,柯尼希定理斷言:矩陣的線秩等於項秩,另外,矩陣的線秩等於該矩陣的具有非零積和式的子方陣的最大階數,亦等於矩陣經行或列的置換,具有全1主對角線的子方陣的最大階數。
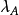
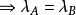
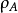

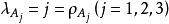
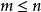





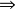





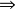
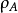
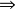
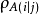




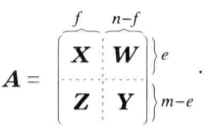



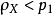



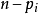
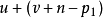

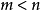
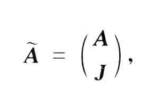


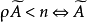
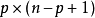



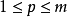

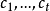






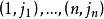


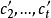
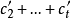





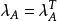





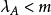
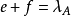
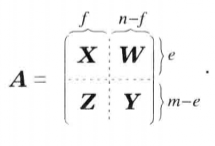
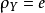
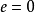
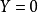

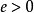
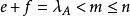
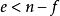




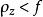
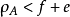

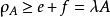
線秩(line rank)是矩陣的一個指標,設A是(0,1)矩陣,A的行與列統稱為線,包含A的全部1的最小線數稱為A的線秩,柯尼希定理斷言:矩陣的線秩等於項秩,另外,...
秩是線性代數術語,線上性代數中,一個矩陣A的列秩是 A的線性無關的縱列的極大數目。類似地,行秩是 A的線性無關的橫行的極大數目。矩陣的列秩和行秩總是相等...
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數,通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A的...
“秩”字從禾,從失;“禾”指五穀、俸祿,“失”意為“動態排序”。“禾”與“失”聯合起來表示“官員俸祿的動態排序”。本義:根據功過確定的官員俸祿。引申義...
秩統計量(rank statistic)是用於統計檢驗的一種統計量。使用秩統計量的統計方法為秩統計方法,或簡稱秩方法。秩方法主要用於統計檢驗,稱為秩檢驗。秩方法最主要的...
向量組的秩為線性代數的基本概念,它表示的是一個向量組的極大線性無關組所含向量的個數。由向量組的秩可以引出矩陣的秩的定義。...
設A是n階矩陣, 若r(A) = n, 則稱A為滿秩矩陣。但滿秩不局限於n階矩陣。若矩陣秩等於行數,稱為行滿秩;若矩陣秩等於列數,稱為列滿秩。既是行滿秩又...
局部秩(local rank),數學專業辭彙,指對一個有限生成投射R模的一種刻畫。...... 局部秩 [1] (local rank),數學專業辭彙,指對一個有限生成投射R模的一種刻畫...
線上性代數中,秩-零化度定理給出了一個線性變換或一個矩陣的秩(rank)和零化度(nullity) 之間的關係。...
聖秩是聖事,藉此聖事,耶穌所託付給他宗徒的使命,得以在天主教會中繼續執行,直到世代的終結。故此,它是宗徒職務的聖事。它包括主教職、司祭職、執事職三個等級...
秩消因子分析rank annihilation fa}lor analysi、可用以解決在不考慮其他共存組分的情況下定量混合物中某單組分的一種因子分析技術。要求採用對組分的濃度具有線性...
項秩(term rank)是矩陣的一個指標,設A是m×n的(0,1)矩陣,A中兩兩不在同一線(矩陣的一行或一列都稱為矩陣的一條線)上的1的最大個數稱為A的項秩,A...
這個時間可作為確定工資和獎金、新老產品成本的依據,可作為生產線和工作小組均衡生產的依據。但由於標準工作時間的確定受到員工個人及工作自身特性等多方面的影響,很...
微分輸出秩(differential output rank)非線性控制系統的微分代數方法中為描述輸入輸出關係的一個量.對於給定的非線性控制系統K(y,u)/K,整數p=diff. tr. d0K(...
