基本介紹
- 中文名:線段樹
- 外文名:Segment Tree
- 功能:單點、區間的修改、查詢
- 時間複雜度:log(n)(建樹為O(n))
- 學科:數據結構
- 領域:數據結構
定義,基本結構,實際套用,基本代碼,C++,Pascal,
定義
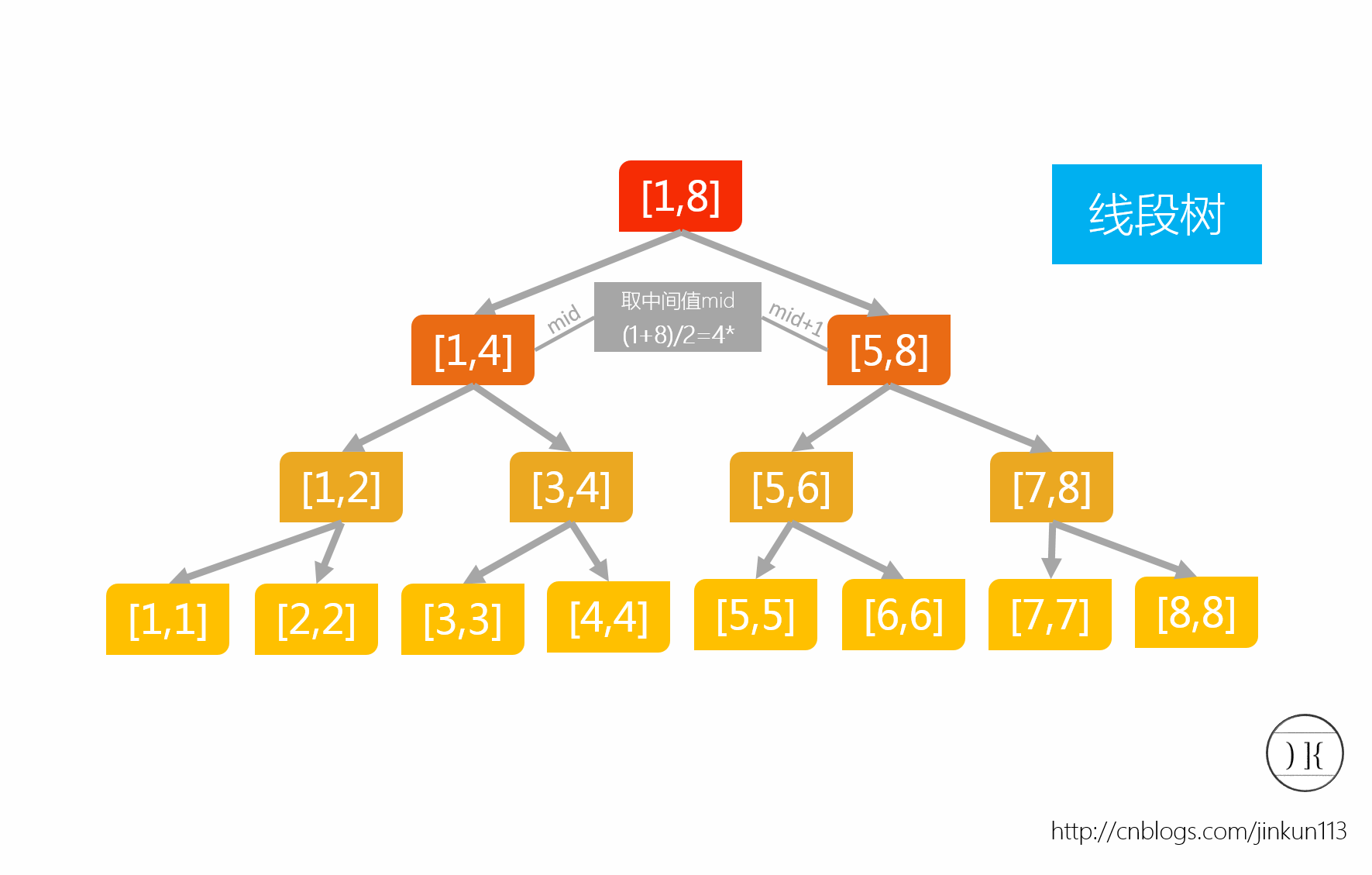
對於線段樹中的每一個非葉子節點[a,b],它的左兒子表示的區間為[a,(a+b)/2],右兒子表示的區間為[(a+b)/2+1,b]。因此線段樹是平衡二叉樹,最後的子節點數目為N,即整個線段區間的長度。
基本結構
線段樹是建立在線段的基礎上,每個結點都代表了一條線段[a,b]。長度為1的線段稱為元線段。非元線段都有兩個子結點,左結點代表的線段為[a,(a + b) / 2],右結點代表的線段為[((a + b) / 2)+1,b]。
下圖就是兩棵長度範圍為[1,5][1,10]的線段樹。
長度範圍為[1,L] 的一棵線段樹的深度為log (L) + 1。這個顯然,而且存儲一棵線段樹的空間複雜度為O(L)。
線段樹支持最基本的操作為插入和刪除一條線段。下面以插入為例,詳細敘述,刪除類似。
將一條線段[a,b] 插入到代表線段[l,r]的結點p中,如果p不是元線段,那么令mid=(l+r)/2。如果b<mid,那么將線段[a,b] 也插入到p的左兒子結點中,如果a>mid,那么將線段[a,b] 也插入到p的右兒子結點中。
插入(刪除)操作的時間複雜度為O(logn)。
實際套用
上面的都是些基本的線段樹結構,但只有這些並不能做什麼,就好比一個程式有輸入沒輸出,根本沒有任何用處。
最簡單的套用就是記錄線段是否被覆蓋,隨時查詢當前被覆蓋線段的總長度。那么此時可以在結點結構中加入一個變數int count;代表當前結點代表的子樹中被覆蓋的線段長度和。這樣就要在插入(刪除)當中維護這個count值,於是當前的覆蓋總值就是根節點的count值了。
另外也可以將count換成bool cover;支持查找一個結點或線段是否被覆蓋。
實際上,通過在結點上記錄不同的數據,線段樹還可以完成很多不同的任務。例如,如果每次插入操作是在一條線段上每個位置均加k,而查詢操作是計算一條線段上的總和,那么在結點上需要記錄的值為sum。
這裡會遇到一個問題:為了使所有sum值都保持正確,每一次插入操作可能要更新O(N)個sum值,從而使時間複雜度退化為O(N)。
解決方案是Lazy思想:對整個結點進行的操作,先在結點上做標記,而並非真正執行,直到根據查詢操作的需要分成兩部分。
根據Lazy思想,我們可以在不代表原線段的結點上增加一個值toadd,即為對這個結點,留待以後執行的插入操作k值的總和。對整個結點插入時,只更新sum和toadd值而不向下進行,這樣時間複雜度可證明為O(logN)。
對一個toadd值為0的結點整個進行查詢時,直接返回存儲在其中的sum值;而若對toadd不為0的一部分進行查詢,則要更新其左右子結點的sum值,然後把toadd值傳遞下去,再對這個查詢本身,左右子結點分別遞歸下去。時間複雜度也是O(nlogN)。
基本代碼
C++
支持以下操作
1 x 若x不存在,插入x
2 x 若x存在,刪除x
3 輸出當前最小值,若不存在輸出-1
4 輸出當前最大值,若不存在輸出-1
5 x 輸出x的前驅,若不存在輸出-1
6 x 輸出x的後繼,若不存在輸出-1
7 x 若x存在,輸出1,否則輸出-1
//by hzwer#include<iostream>#include<cstdio>#include<cstring>#include<cstdlib>#include<algorithm>#include<cmath>#include<map>#include<set>#include<vector>#include<queue>#define inf 1000000000using namespace std;int n,m;struct seg{int l,r,v;}t[3000005];void build(int k,int l,int r) //建樹 k:當前節點下標 線段左為l,線段右為r{ t[k].l=l;t[k].r=r; //線段左端,線段右端 if(l==r)return; //線段長度為零,結束 int mid=(l+r)>>1; //取線段中點 build(k<<1,l,mid); //k<<1:下標為k節點的左兒子下標,線段左為l,線段右為mid k<<1==k*2 build(k<<1|1,mid+1,r); //k<<1|1:下標為k節點的右兒子下標,線段左為mid+1,線段右為r k<<1|1==k*2+1}int mn(int k){ if(!t[k].v)return -1; int l=t[k].l,r=t[k].r; if(l==r)return l; if(t[k<<1].v)return mn(k<<1); else return mn(k<<1|1);}int mx(int k){ if(!t[k].v)return -1; int l=t[k].l,r=t[k].r; if(l==r)return l; if(t[k<<1|1].v)return mx(k<<1|1); else return mx(k<<1);}void insert(int k,int val){ int l=t[k].l,r=t[k].r; if(l==r){t[k].v=1;return;} int mid=(l+r)>>1; if(val<=mid)insert(k<<1,val); else insert(k<<1|1,val); t[k].v=t[k<<1].v+t[k<<1|1].v;}int find(int k,int val){ int l=t[k].l,r=t[k].r; if(l==r) { if(t[k].v)return 1; return -1; } int mid=(l+r)>>1; if(val<=mid)return find(k<<1,val); else return find(k<<1|1,val);}void del(int k,int val){ int l=t[k].l,r=t[k].r; if(l==r){t[k].v=0;return;} int mid=(l+r)>>1; if(val<=mid)del(k<<1,val); else del(k<<1|1,val); t[k].v=t[k<<1].v+t[k<<1|1].v;}int findpr(int k,int val){ if(val<0)return -1; if(!t[k].v)return -1; int l=t[k].l,r=t[k].r; if(l==r)return l; int mid=(l+r)>>1; if(val<=mid)return findpr(k<<1,val); else { int t=findpr(k<<1|1,val); if(t==-1)return mx(k<<1); else return t; }}int findsu(int k,int val){ if(!t[k].v)return -1; int l=t[k].l,r=t[k].r; if(l==r)return l; int mid=(l+r)>>1; if(val>mid)return findsu(k<<1|1,val); else { int t=findsu(k<<1,val); if(t==-1)return mn(k<<1|1); else return t; }}int main(){ scanf("%d %d",&n,&m); build(1,0,n); int opt,x; for(int i=1;i<=m;i++) { scanf("%d",&opt); switch(opt) { case 1:scanf("%d",&x);if(find(1,x)==-1)insert(1,x);break; case 2:scanf("%d",&x);if(find(1,x)==1)del(1,x);break; case 3:printf("%d\n",mn(1));break; case 4:printf("%d\n",mx(1));break; case 5:scanf("%d",&x);printf("%d\n",findpr(1,x-1));break; case 6:scanf("%d",&x);printf("%d\n",findsu(1,x+1));break; case 7:scanf("%d",&x);printf("%d\n",find(1,x));break; } } return 0;}Pascal
基本操作
program intervaltree;const maxn = 10000; inf = 'input.txt'; ouf = 'output.txt';type treenode = record a, b, Left, Right, cover: longint; end;var tree: array[1..maxn] of treenode; number, tot, c, d: longint;procedure maketree(a, b: longint);var now: longint;begin Inc(tot); now := tot; tree[now].a := a; tree[now].b := b; tree[now].cover := 0; if a + 1 < b then begin tree[now].Left := tot + 1; maketree(a, (a + b) div 2); tree[now].Right := tot + 1; maketree((a + b) div 2, b); end;end;procedure insert(num: longint);begin if (c <= tree[num].a) and (tree[num].b <= d) then tree[num].cover := tree[num].cover + 1 else begin if c < (tree[num].a + tree[num].b) div 2 then insert(tree[num].Left); if d > (tree[num].a + tree[num].b) div 2 then insert(tree[num].Right); end;end;procedure Delete(num: longint);begin if (c <= tree[num].a) and (tree[num].b <= d) then Dec(tree[num].cover) else begin if c < (tree[num].a + tree[num].b) div 2 then Delete(tree[num].Left); if d > (tree[num].a + tree[num].b) div 2 then Delete(tree[num].Right); end;end;procedure Count(num: longint);begin if tree[num].cover > 0 then number := number + (tree[num].b - tree[num].a) else begin if tree[num].Left > 0 then Count(tree[num].Left); if tree[num].Right > 0 then Count(tree[num].Right); end;end;begin Assign(input, inf); Reset(input); Assign(output, ouf); Rewrite(output); Readln(c, d); maketree(c, d); while not EOF do begin Readln(c, d); insert(1); end; Count(1); Writeln(number); Close(output); Close(input);end.