樹狀數組

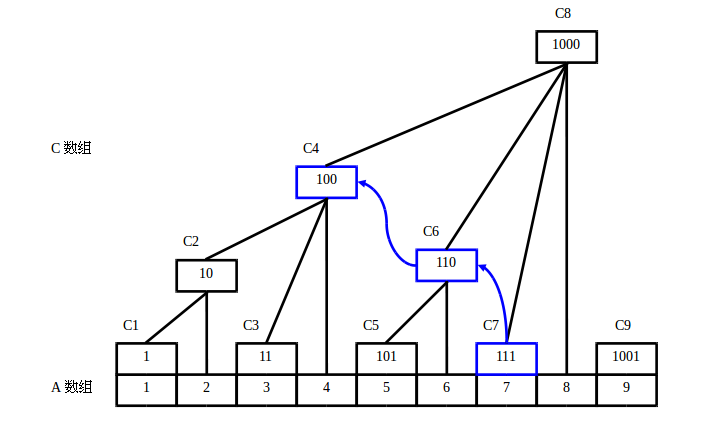
樹狀數組(Binary Indexed Tree(B.I.T), Fenwick Tree)是一個查詢和修改複雜度都為log(n)的數據結構。主要用於查詢任意兩位之間的所有元素之和，但是每次只能修改一個元素的值；經過簡單修改可以在log(n)的複雜度下進行範圍修改，但是這時只能查詢其中一個元素的值(如果加入多個輔助數組則可以實現區間修改與區間查詢)。

這種數據結構（算法）並沒有C++和Java的庫支持，需要自己手動實現。在Competitive Programming的競賽中被廣泛的使用。樹狀數組和線段樹很像，但能用樹狀數組解決的問題，基本上都能用線段樹解決，而線段樹能解決的樹狀數組不一定能解決。相比較而言，樹狀數組效率要高很多。

基本介紹

• 中文名：樹狀數組
• 套用範圍：信息學
• 功能：區間和查詢、單點修改
• 時間複雜度：log（n）

樹狀圖概念

假設數組a[1..n]，那么查詢a[1]+...+a[n]的時間是log級別的，而且是一個線上的數據結構，支持隨時修改某個元素的值，複雜度也為log級別。

來觀察這個圖：

令這棵樹的結點編號為C1，C2...Cn。令每個結點的值為這棵樹的值的總和，那么容易發現：

C1 = A1

C2 = A1 + A2

C3 = A3

C4 = A1 + A2 + A3 + A4

C5 = A5

C6 = A5 + A6

C7 = A7

C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

...

C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16

這裡有一個有趣的性質：

設節點編號為x，那么這個節點管轄的區間為2^k（其中k為x二進制末尾0的個數）個元素。因為這個區間最後一個元素必然為Ax，

所以很明顯：Cn = A(n – 2^k + 1) + ... + An

算這個2^k有一個快捷的辦法，定義一個函式如下即可：

int lowbit(int x){return x&(x^(x–1));}

利用機器補碼特性，也可以寫成：

int lowbit(int x){return x&-x;}

當想要查詢一個SUM(n)(求a[n]的和），可以依據如下算法即可：

step1:　令sum = 0，轉第二步；

step2:　假如n <= 0，算法結束，返回sum值，否則sum = sum + Cn，轉第三步；

step3: 令n = n – lowbit(n)，轉第二步。

可以看出，這個算法就是將這一個個區間的和全部加起來，為什麼是效率是log(n)的呢？以下給出證明：

n = n – lowbit(n)這一步實際上等價於將n的二進制的最後一個1減去。而n的二進制里最多有log(n)個1，所以查詢效率是log(n)的。

那么修改呢，修改一個節點，必須修改其所有祖先，最壞情況下為修改第一個元素，最多有log(n)的祖先。

所以修改算法如下（給某個結點i加上x）：

step1: 當i > n時，算法結束，否則轉第二步；

step2: Ci = Ci + x， i = i + lowbit(i)轉第一步。

i = i +lowbit(i)這個過程實際上也只是一個把末尾1補為0的過程。

對於數組求和來說樹狀數組簡直太快了!

註：

求lowbit(x)的建議公式：

lowbit(x):=x and -x;

或lowbit(x):=x and (x xor (x - 1));

lowbit(x)即為2^k的值。

充分性

很容易知道C8表示A1～A8的和，但是C6卻是表示A5～A6的和，為什麼會產生這樣的區別的呢？或者說發明她的人為什麼這樣區別對待呢？

樹狀數組線性圖

答案是，這樣會使操作更簡單！看到這相信有些人就有些感覺了，為什麼複雜度被log了呢？可以看到，C8可以看作A1～A8的左半邊和+右半邊和，而其中左半邊和是確定的C4，右半邊其實也是同樣的規則把A5～A8一分為二……繼續下去都是一分為二直到不能分樹狀數組巧妙地利用了二分，樹狀數組並不神秘，關鍵是巧妙！

結構體版

#include<iostream>#include<vector>using namespace std;class BinTree:vector<int>{    public:        explicit BinTree(int k=0)//默認初始化一個能保存k個元素的空樹狀數組        {            assign(k+1,0);//有效下標從1開始，0僅作邏輯用處        }        int lowbit(int k)        {            return k&-k;            //也可寫作x&(x^(x–1))        }        int sum(int k)//求第1個元素到第n個元素的和        {            return k>0?sum(k-lowbit(k))+(*this)[k]:0;        }        int last()//返回最後一個元素下標        {            return size()-1;        }        void add(int k,int w)//為節點k加上w        {            if(k>last())return;            (*this)[k]+=w;            add(k+lowbit(k),w);        }};int main(){    BinTree test(123);    test.add(27,72);    cout<<test.sum(26)<<' '<<test.sum(27)<<' '<<test.sum(123);}

函式版

#include<iostream>using namespace std;int n,m,i,num[100001],t[200001],l,r;//num:原數組；t：樹狀數組 int lowbit(int x){    return x&(-x);}void change(int x,int p)//將第x個數加p {    while(x<=n)    {        t[x]+=p;        x+=lowbit(x);    }    return;}int sum(int k)//前k個數的和 {    int ans=0;    while(k>0)    {        ans+=t[k];        k-=lowbit(k);    }    return ans;}int ask(int l,int r)//求l-r區間和 {    return sum(r)-sum(l-1); }int main(){    cin>>n>>m;    for(i=1;i<=n;i++)    {        cin>>num[i];        change(i,num[i]);    }    for(i=1;i<=m;i++)    {        cin>>l>>r;        cout<<ask(l,r)<<endl;    }    return 0;}

典題分析

例題1

給定一個初始值都為0的序列,動態地修改一些位置上的數字,加上一個數,減去一個數,或者乘上一個數,然後動態地提出問題,問題的形式是求出一段數字的和.

算法分析

如果直接做的話,修改的複雜度是O(1),詢問的複雜度是O(N),M次詢問的複雜度是M*N.M,N的範圍可以有100000以上,所以這樣做會逾時,但是如果用線段樹的話,還是很不錯的! 有很多線段樹能實現但樹狀數組卻實現不了的題目。

線段樹解法分析

可以看出,這棵樹的構造用二分便可以實現.複雜度是2*N.

每個結點用數組a來表示該結點所表示範圍內的數據之和.

修改一個位置上數字的值,就是修改一個葉子結點的值,而當程式由葉子結點返回根節點的同時順便修改掉路徑上的結點的a數組的值.

對於詢問的回答,可以直接查找i..j範圍內的值,遇到分叉時就兵分兩路,最後在合起來.也可以先找出0..i-1的值和0..j的值,兩個值減一減就行了.後者的實際操作次數比前者小一些.

這樣修改與維護的複雜度是logN.詢問的複雜度也是logN,對於M次詢問,複雜度是MlogN.

然而不難發現,線段樹的編程複雜度大,空間複雜度大,時間效率也不高!!!!

所以我們來想用樹形數組來實現:

那么,何為樹形數組呢??

C數組就是樹狀數組,a數組是原數組;

對於序列a，我們設一個數組C定義C[t] = a[t – 2^k + 1] + … + a[t]，k為t在二進制下末尾0的個數。

K的計算可以這樣:

2^k=t and (t xor (t-1))

以6為例

(6)10=(0110)2

xor 6-1=(5)10=(0101)2

(0011)2

and (6)10=(0110)2

(0010)2

所以問題變的很簡單,重要寫幾個函式就可以了;

求2^k的函式代碼如下:

int Lowbit(int t){return t&(t^(t-1));}FunctionLowbit(t:longint):longint;BeginLowbit:=tand(txor(t-1));End;

求1 -- end和的函式代碼如下:

intSum(intend){intsum=0;while(end>0){sum+=in[end];end-=Lowbit(end);}returnsum;}FunctionSum(tail:longint):longint;Vars:longint;Begins:=0;whiletail>0dobegininc(s,in[tail]);dec(tail,Lowbit(tail));end;sum:=s;End;

對某位進行操作函式如下(以加法為例)

void plus(int pos,int num){while(pos<=n){in[pos]+=num;pos+=Lowbit(pos);}}Procedureplus(p,num:longint);Beginwhilep<=ndobegininc(in[p],num);inc(p,Lowbit(p));end;End.

有了這三個函式整個樹形數組也就基本構建成功啦!!

對於剛才的一題,每次修改與詢問都是對C數組做處理.空間複雜度有3N降為N,時間效率也有所提高.編程複雜度更是降了不少.

對於lowbit可有最佳化 P :lowbit:=X AND(not x+1){或 X AND (-X)}; C: lowbit:=x &(-x){或 x & (~x+1)};

例題2

求n個數中 k組提問 從t到t1個數字之和

pascal代碼

programBIT_test;uses sysutils;var a,c:array[1..100000]oflongint;    n:longint;    ch:char;    i,k,t,t1:longint;    ti:double;//計時用functionLow_bit(x:longint):longint;//取出x在二進制下最右邊一個1begin  exit(x and (-x));end;procedure Modify(pos,x:longint);//改變數據begin  while pos<=n do begin    inc(c[pos],x);    inc(pos,low_bit(pos))  end;end;function sum(pos:longint):longint;//1..pos求和begin  sum:=0;  while pos>0 do begin    inc(sum,c[pos]);    dec(pos,low_bit(pos));  end;end;begin  readln(n);  for i:=1 to n do begin    read(a[i]);    Modify(i,a[i]);  end;  readln;  ti:=now;  readln(k);  for i:=1 to k do begin    readln(t,t1);    writeln(sum(t1)-sum(t-1));  end;  writeln((now-ti)*86400*1000:0:0,'MS');end.

線段樹的比較

樹狀數組是一個可以很高效的進行區間統計的數據結構。在思想上類似於線段樹，比線段樹節省空間，編程複雜度比線段樹低，但適用範圍比線段樹小。

以簡單的求和為例。設原數組為a[1..N]，樹狀數組為c[1..N]，其中c[k] = a[k-(2^t)+1] + ... + a[k]。比如c[6] = a[5] + a[6]。也就是說，把k表示成二進制1***10000，那么c[k]就是1***00001 + 1***00010 + ... + 1***10000這一段數的和。設一個函式lowestbit(k)為取得k的最低非零位，容易發現，根據上面的表示方法，從a[1]到a[k]的所有數的總和即為sum[k] = c[k] + c[k-lowestbit(k)] + c[k-lowestbit(k)-lowestbit(k-lowestbit(k))] + ... 於是可以在logk的時間內求出sum[k]。當數組中某元素髮生變化時，需要改動的c值是c[k],c[k+lowestbit(k)], c[k+lowestbit(k)+lowestbit(k+lowestbit(k))] ... 這個複雜度是logN (N為最大範圍)

擴展到多維情況：以二維為例，用c[k1][k2]表示c[k1-(2^t1)+1][k2-(2^t2)+1] + ... + c[k1][k2]的總和。可以用類似的方法進行處理。複雜度為(logn)^k (k為維數)

樹狀數組相比線段樹的優勢：空間複雜度略低，編程複雜度低，容易擴展到多維情況。劣勢：適用範圍小，對可以進行的運算也有限制，比如每次要查詢的是一個區間的最小值，似乎就沒有很好的解決辦法。

多維情況的幾道題目:

URAL 1470 UFOs

POJ 2155 Matrix

表面上看，這題的要求似乎和樹狀數組的使用方法恰好相反，改變的是一個區間，查詢的反而是一個點。實際上可以通過一個轉化巧妙的解決。

首先對於每個數A定義集合up(A)表示{A, A+lowestbit(A), A+lowestbit(A)+lowestbit(A+lowestbit(A))...} 定義集合down(A)表示{A, A-lowestbit(A), A-lowestbit(A)-lowestbit(A-lowestbit(A)) ... , 0}。可以發現對於任何A<B，up(A)和down(B)的交集有且僅有一個數。

於是對於這道題目來說，翻轉一個區間[A,B]（為了便於討論先把原問題降為一維的情況），我們可以把down(B)的所有元素的翻轉次數+1，再把down(A-1)的所有元素的翻轉次數-1。而每次查詢一個元素C時，只需要統計up(C)的所有元素的翻轉次數之和，即為C實際被翻轉的次數。

實際實現時，由於只考慮奇偶，因此無須統計確切的翻轉次數。另外，如果翻轉up(A)和up(B+1)，查詢down(C)，也是同樣的效果。這種方法可以很容易地擴展到二維情況。比起線段樹、四分樹之類的常規思路，無論編程複雜度還是常數速度上都有很大優勢。

#include<cstdio>#include<iostream>#include<cstring>#include<cstdlib>int x,n,t;char ques[5];int tree[1500][1500];using namespace std;int lowbit(int a){    return a&-a;}void change(int x,int y){    for(int i=x;i<=n;i+=lowbit(i))    {        for(int j=y;j<=n;j+=lowbit(j))        {        tree[i][j]++;        }}return;}int getsum(int x,int y){    int ans=0;    for (int i=x;i>=1;i-=lowbit(i))    {        for(int j=y;j>=1;j-=lowbit(j))        {            ans+=tree[i][j];        }    }    return ans;}int main(){    scanf ("%d",&x);    for (int i=1;i<=x;i++)    {        scanf ("%d%d\n",&n,&t);        memset(tree,0,sizeof(tree));        for (int i=1;i<=t;i++)        {            scanf ("%s",&ques);            if (ques[0]=='C')            {                int x1,x2,y1,y2;                scanf ("%d%d%d%d",&x1,&y1,&x2,&y2);                change(x1,y1);                change(x2+1,y1);                change(x1,y2+1);                change(x2+1,y2+1);            }            if (ques[0]=='Q')            {                int x,y;                scanf ("%d%d",&x,&y);                printf ("%d\n",getsum(x,y)%2);            }        }        printf ("\n");    }    return 0;}