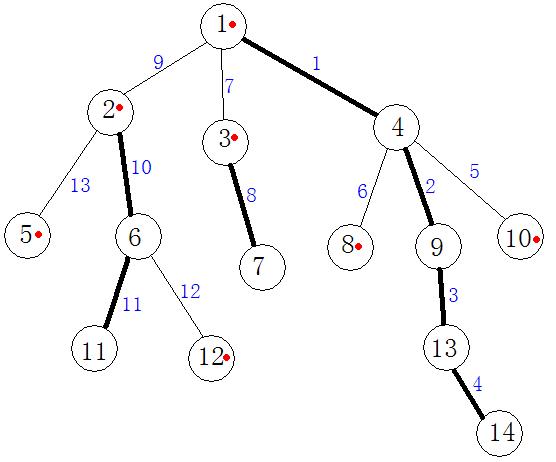
樹鏈剖分,計算機術語,指一種對樹進行劃分的算法,它先通過輕重邊剖分將樹分為多條鏈,保證每個點屬於且只屬於一條鏈,然後再通過數據結構(樹狀數組、BST、SPLAY、線段樹等)來維護每一條鏈。
基本介紹
- 中文名:樹鏈剖分
- 分類:計算機術語
- 類別:一種對樹進行劃分的算法
- 常見作用:維護樹路徑的信息
基本定義,方法,具體步驟,經典算法題目,
基本定義
樹路徑信息維護算法。
將一棵樹劃分成若干條鏈,用數據結構去維護每條鏈,複雜度為O(logN)。
其實本質是一些數據結構/算法在樹上的推廣
方法
常見的路徑剖分的方法是輕重樹鏈剖分(啟發式剖分)
將樹中的邊分為:輕邊和重邊 定義size(X)為以X為根的子樹的節點個數。 令V為U的兒子節點中size值最大的節點,那么邊(U,V)被稱為重邊,樹中重邊之外的邊被稱為輕邊。
性質:輕邊(U,V),size(V)<=size(U)/2。 從根到某一點的路徑上,不超過O(logN)條輕邊,不超過O(logN)條重路徑。
具體步驟
預處理
第一遍dfs求出樹每個結點的深度deep[x],其為根的子樹大小size[x]
以及祖先的信息fa[x][i]表示x往上距離為2^i的祖先
第二遍dfs
根節點為起點,向下拓展構建重鏈
選擇最大的一個子樹的根繼承當前重鏈
其餘節點,都以該節點為起點向下重新拉一條重鏈
給每個結點分配一個位置編號,每條重鏈就相當於一段區間,用數據結構去維護。
把所有的重鏈首尾相接,放到同一個數據結構上,然後維護這一個整體即可
修改操作
1、單獨修改一個點的權值
根據其編號直接在數據結構中修改就行了。
2、修改點u和點v的路徑上的權值
(1)若u和v在同一條重鏈上
直接用數據結構修改pos[u]至pos[v]間的值。
(2)若u和v不在同一條重鏈上
一邊進行修改,一邊將u和v往同一條重鏈上靠,然後就變成了情況(1)。
偽代碼
CHANGE (x, y ,d)
while top[x]≠top[y]
do if dep[top[x]]<dep[top[y]]
then SWAP(x,y), SWAP (gx,gy)
CHANGE-IT(tid[top[x]],tid[x],d)
fa[x]→x
if dep[x]>dep[y]
then SWAP (x,y)
CHANGE-IT(tid[x],tid[y],d)
//CHANGE-IT(l,r,d)為數據結構的修改操作:將區間[l,r]上的所有權值改為d
查詢操作
查詢操作的分析過程同修改操作
偽代碼
QUERY (x, y)
while top[x]≠top[y]
do if dep[top[x]]<dep[top[y]]
then SWAP (x,y), SWAP (gx,gy)
QUERY-IT(tid[top[x]],tid[x])
fa[x]→x
if dep[x]>dep[y]
then SWAP (x,y)
QUERY-IT(tid[x],tid[y])
//QUERY-IT(l,r)為數據結構的查詢操作,
題目不同,選用不同的數據結構來維護值,通常有線段樹和splay
經典算法題目
ZJOI2008樹的統計
I. CHANGE u t : 把結點u的權值改為t
II. QMAX u v: 詢問從點u到點v的路徑上的節點的最大權值
III. QSUM u v: 詢問從點u到點v的路徑上的節點的權值和
注意:從點u到點v的路徑上的節點包括u和v本身
附代碼
//by hzwer#include<iostream>#include<cstdio>#include<cstring>#define inf 0x7fffffff#define N 30005 #define M 60005using namespace std;int n,q,cnt,sz;int fa[N][15],v[N],deep[N],size[N],head[N];int pos[N],belong[N];bool vis[N];struct data{int to,next;}e[M];struct seg{int l,r,mx,sum;}t[100005];void insert(int u,int v){ e[++cnt].to=v;e[cnt].next=head[u];head[u]=cnt; e[++cnt].to=u;e[cnt].next=head[v];head[v]=cnt;}void ini(){ scanf("%d",&n); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); insert(x,y); } for(int i=1;i<=n;i++)scanf("%d",&v[i]);}void dfs1(int x){ size[x]=1;vis[x]=1; for(int i=1;i<=14;i++) { if(deep[x]<(1<<i))break; fa[x][i]=fa[fa[x][i-1]][i-1];//倍增處理祖先信息 } for(int i=head[x];i;i=e[i].next) { if(vis[e[i].to])continue; deep[e[i].to]=deep[x]+1; fa[e[i].to][0]=x; dfs1(e[i].to); size[x]+=size[e[i].to]; }}void dfs2(int x,int chain){ int k=0;sz++; pos[x]=sz;//分配x結點線上段樹中的編號 belong[x]=chain; for(int i=head[x];i;i=e[i].next) if(deep[e[i].to]>deep[x]&&size[e[i].to]>size[k]) k=e[i].to;//選擇子樹最大的兒子繼承重鏈 if(k==0)return; dfs2(k,chain); for(int i=head[x];i;i=e[i].next) if(deep[e[i].to]>deep[x]&&k!=e[i].to) dfs2(e[i].to,e[i].to);//其餘兒子新開重鏈}int lca(int x,int y)//求lca{ if(deep[x]<deep[y])swap(x,y); int t=deep[x]-deep[y]; for(int i=0;i<=14;i++) if(t&(1<<i))x=fa[x][i]; for(int i=14;i>=0;i--) if(fa[x][i]!=fa[y][i]) {x=fa[x][i];y=fa[y][i];} if(x==y)return x; else return fa[x][0];}void build(int k,int l,int r)//建線段樹{ t[k].l=l;t[k].r=r; if(l==r)return; int mid=(l+r)>>1; build(k<<1,l,mid); build(k<<1|1,mid+1,r);}void change(int k,int x,int y)//線段樹單點修改{ int l=t[k].l,r=t[k].r,mid=(l+r)>>1; if(l==r){t[k].sum=t[k].mx=y;return;} if(x<=mid)change(k<<1,x,y); else change(k<<1|1,x,y); t[k].sum=t[k<<1].sum+t[k<<1|1].sum; t[k].mx=max(t[k<<1].mx,t[k<<1|1].mx);}int querysum(int k,int x,int y)//線段樹區間求和{ int l=t[k].l,r=t[k].r,mid=(l+r)>>1; if(l==x&&y==r)return t[k].sum; if(y<=mid)return querysum(k<<1,x,y); else if(x>mid)return querysum(k<<1|1,x,y); else {return querysum(k<<1,x,mid)+querysum(k<<1|1,mid+1,y);}}int querymx(int k,int x,int y)//線段樹區間求最大值{ int l=t[k].l,r=t[k].r,mid=(l+r)>>1; if(l==x&&y==r)return t[k].mx; if(y<=mid)return querymx(k<<1,x,y); else if(x>mid)return querymx(k<<1|1,x,y); else {return max(querymx(k<<1,x,mid),querymx(k<<1|1,mid+1,y));}}int solvesum(int x,int f){ int sum=0; while(belong[x]!=belong[f])//不在一條重鏈上就將x跳到鏈首,走一條輕邊,如此反覆 { sum+=querysum(1,pos[belong[x]],pos[x]); x=fa[belong[x]][0]; } sum+=querysum(1,pos[f],pos[x]); return sum;}int solvemx(int x,int f){ int mx=-inf; while(belong[x]!=belong[f]) { mx=max(mx,querymx(1,pos[belong[x]],pos[x])); x=fa[belong[x]][0]; } mx=max(mx,querymx(1,pos[f],pos[x])); return mx;}void solve(){ build(1,1,n); for(int i=1;i<=n;i++) change(1,pos[i],v[i]); scanf("%d",&q);char ch[6]; for(int i=1;i<=q;i++) { int x,y;scanf("%s%d%d",ch,&x,&y); if(ch[0]=='C'){v[x]=y;change(1,pos[x],y);} else { int t=lca(x,y); if(ch[1]=='M') printf("%d\n",max(solvemx(x,t),solvemx(y,t))); else printf("%d\n",solvesum(x,t)+solvesum(y,t)-v[t]); } }}int main(){ ini(); dfs1(1); dfs2(1,1); solve(); return 0;}