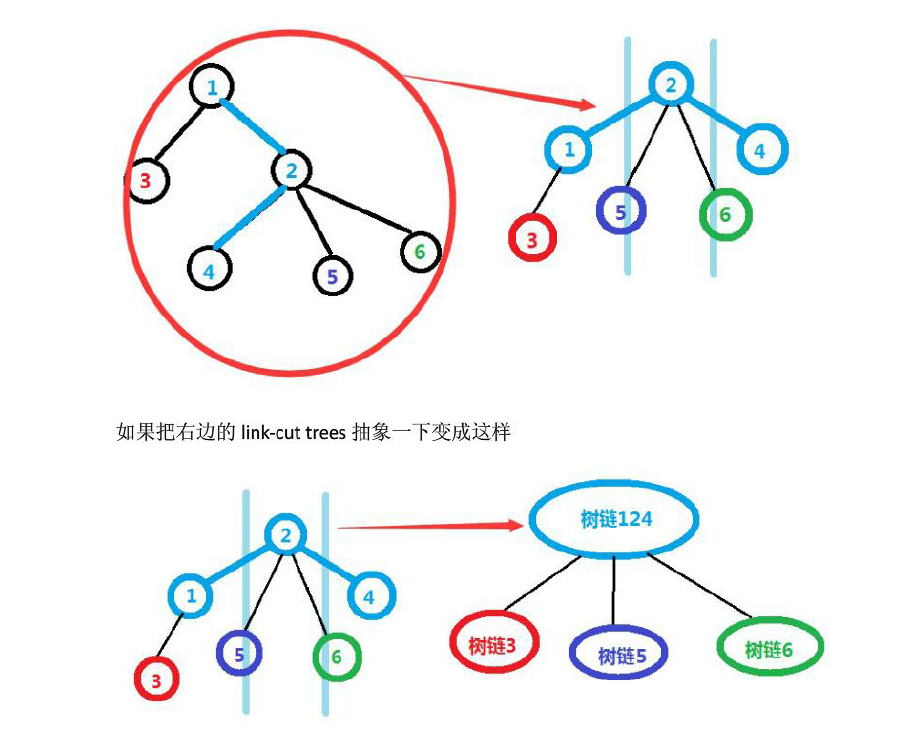
基本介紹
- 中文名：動態樹問題
- 算法：Link-Cut Trees，splay
- 創始人：Sleator 和Tarjan
- 時間複雜度：O((n + q) log n)
定義,問題描述,出現,解法,實例套用,
定義
動態樹問題, 即要求我們維護一個由若干棵子結點無序的有根樹組成的森林，支持對樹的分割, 合併, 對某個點到它的根的路徑的某些操作, 以及對某個點的子樹進行的某些操作。
問題描述
維護一個數據結構, 支持以下操作:
- 查詢一個點的父親
- 查詢一個點所在的樹的根
- 修改某個節點的權
- 向從某個節點到它所在的樹的根的路徑上的所有的節點的權增加一個數
- 查詢從某個節點到它所在的樹的根的路徑上的所有的節點的權的最小值
- 把一棵樹從某個節點和它的父親處斷開，使其成為兩棵樹
- 讓一棵樹的根成為另一棵樹的某個節點的兒子，從而合併這兩棵樹
- 把某棵樹的根修改為它的某個節點
- 查詢在同一棵樹上的兩個節點的LCA
- 修改以某個節點為根的子樹的所有節點的權
- 查詢以某個節點為根的子樹的所有節點的權的最小值
出現
動態樹問題在OI中還是近幾年興起的。很多資料中將“動態樹”特指為link-cut-tree這種數據結構，而事實上動態樹是一類問題的通稱，說白了就是上文中各種數列的維護改到樹上來做，例如查詢鏈上和、子樹和、修改節點數值等等。
處理這一類問題的最基本思路就是將樹上的問題重新轉化到鏈上，然後套用上文中的各種方法進行解決，而這種轉化往往是基於給樹上的節點按照某種順序標號，然後每次處理標號連續的一段或若干段。
而另外一些涉及樹的形態變化的問題則難以利用這種“標號”的思路進行維護（因為一個簡單的修改可能會導致整棵樹的標號出現不規則的更改）。為了解決這些問題，以RobertE.Tarjan為首的科學家們研究出各種實用的、具有良好理論複雜度和較大常數的數據結構，直接對樹的形態進行維護。本部分會簡要介紹DFS序和樹鏈剖分兩種標號法和link-cut-tree的套用，理論部分的最後會提及LCT解決子樹問題的一個方案（自調整TopTree）。然後以幾道經典題為本文畫上句號。
解法
旋轉及連線函式
樹結構的基礎操作之一，可完成節點的旋轉操作。
void link(node *f,node *x,bool d){ f->s[d]=x; if(x) x->p=f; update(f);}bool is_root(node *now){return !now->p||now!=now->p->s[0]&&now!=now->p->s[1];}void rotate(node *now,bool d){ node *x=now->s[d],*p=now->p; bool flag=is_root(now); link(now,x->s[d^1],d); link(x,now,d^1); if(flag) x->p=p; else link(p,x,now==p->s[1]);}splay
在splay上的一般操作都基於伸展操作：假構想要對一個二叉查找樹執行一系列的查找操作，為了使整個查找時間更小，被查頻率高的那些條目就應當經常處於靠近樹根的位置。於是想到設計一個簡單方法， 在每次查找之後對樹進行重構，把被查找的條目搬移到離樹根近一些的地方。splay應運而生。伸展樹是一種自調整形式的二叉查找樹，它會沿著從某個節點到樹根之間的路徑，通過一系列的旋轉把這個節點搬移到樹根去。
stack<node*>s;void splay(node *now){ s.push(now); for(node *i=now;!is_root(i);i=i->p) s.push(i->p); while(!s.empty()) down(s.top()),s.pop(); while(!is_root(now)) { node *cur=now->p; bool d1=now==cur->s[1]; if(is_root(cur)) { rotate(cur,d1); return; } node *x=cur->p; bool d2=cur==x->s[1]; if(d1^d2) rotate(cur,d1),rotate(x,d2); else rotate(x,d2),rotate(cur,d1); }}Access
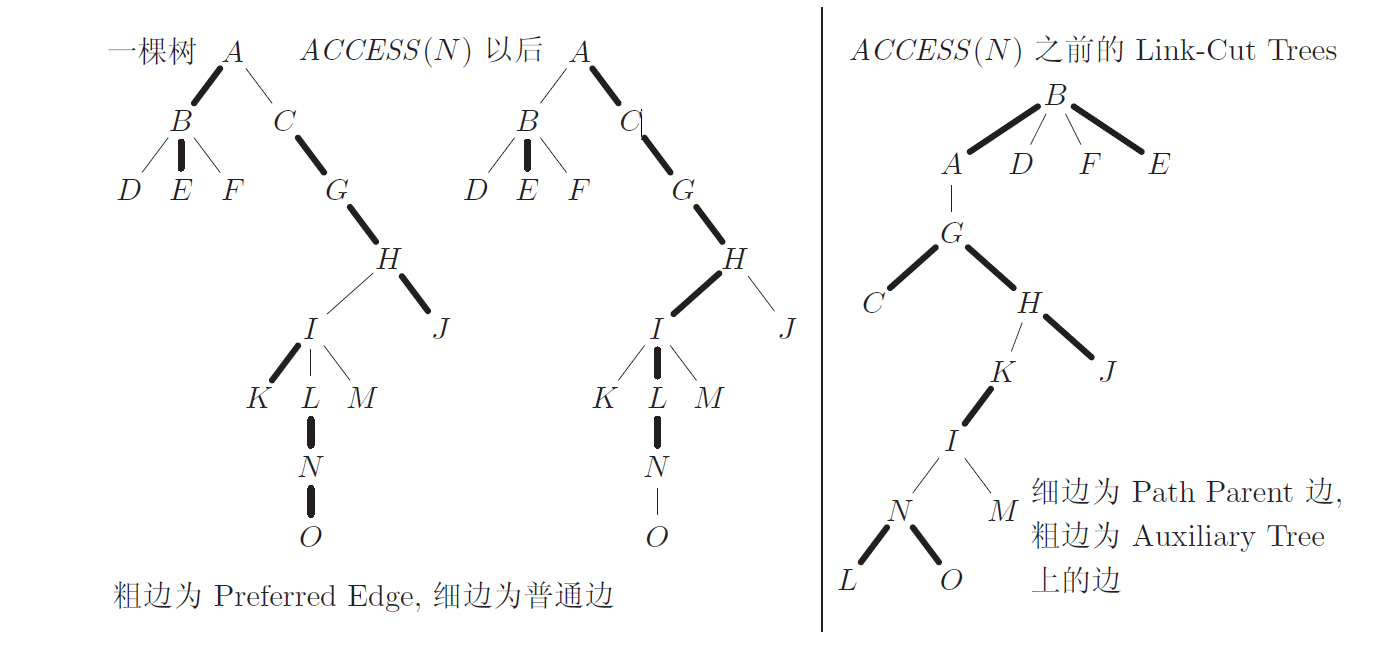ACCESS操作前後對比圖ACCESS 操作是動態樹 的所有操作的基礎. 假設調用了過程ACCESS(v), 那么從點v 到根結點的路徑就成為一條新的鏈. 如果路徑上經過的某個結點u 並不是它的父親節點parent(u) 的子節點, 那么由於parent(u) 的子節點會變為u , 原本包含parent(u) 的Preferred Path將不再包含結點parent(u) 及其之上的部分.
void link(node *f,node *x,bool d){ f->s[d]=x; if(x) x->p=f; update(f);}bool is_root(node *now){return !now->p||now!=now->p->s[0]&&now!=now->p->s[1];}void rotate(node *now,bool d){ node *x=now->s[d],*p=now->p; bool flag=is_root(now); link(now,x->s[d^1],d); link(x,now,d^1); if(flag) x->p=p; else link(p,x,now==p->s[1]);}Find Root
在ACCESS(v) 之後, 根結點一定是v 所屬的splay的最小結點. 我們先把v 旋轉到它所屬的splay的根.。再從v 開始, 沿著splay向左走, 直到不能再向左, 這個點就是我們要找的根結點。由於使用的是Splay Tree數據結構保存splay, 我們還需要對根結點進行Splay操作。
Set Root
在ACCESS(v) 之後, 根結點一定是v 所屬的splay的最小結點. 我們先把v 旋轉到它所屬的splay的根。此時節點v一定是splay深度最小的節點，將整條鏈旋轉就可將v轉到實數的根。考慮到時間複雜度，可以打懶標記。
Cut
先訪問v, 然後把v 旋轉到它所屬的splay的根, 然後再斷開v 在它的所屬splay中與它的左子樹的連線, 並設定
Join
先訪問v , 然後修改v 所屬的splay的Path Parent 為w, 然後再次訪問v。
時間複雜度分析
可以看出, 除ACCESS 操作之外的其它操作, 其均攤時間複雜度至多為O(log n). 所以只用分析ACCESS 的時間複雜度.在ACCESS 操作的分析中, 我們將ACCESS 的時間分為兩部分計算. 第一部分我們證明切換子節點的次數是均攤O(log n) 的; 第二部分我們證明一次ACCESS 中的所有Splay 操作的總時間是均攤O(log n) 的.
實例套用
染色[SDOI2011]
題目描述：
給定一棵有n個節點的無根樹和m個操作，操作有2類：
1、將節點a到節點b路徑上所有點都染成顏色c；
2、詢問節點a到節點b路徑上的顏色段數量（連續相同顏色被認為是同一段），如“112221”由3段組成：“11”、“222”和“1”。
請你寫一個程式依次完成這m個操作。
輸入格式：
第一行包含2個整數n和m，分別表示節點數和運算元；
第二行包含n個正整數表示n個節點的初始顏色
下面行每行包含兩個整數x和y，表示x和y之間有一條無向邊。
下面行每行描述一個操作：
“C a b c”表示這是一個染色操作，把節點a到節點b路徑上所有點（包括a和b）都染成顏色c；
“Q a b”表示這是一個詢問操作，詢問節點a到節點b（包括a和b）路徑上的顏色段數量。
輸出格式：
對於每個詢問操作，輸出一行答案。
參考代碼：
#include<bits/stdc++.h>#define ll long longusing namespace std;const int MAXN=1e5+10;struct node{ int v,upv,downv,sum,lz; bool lz_rev; node *p,*s[2]; void build(int x) { v=upv=downv=x; sum=1; lz=0; lz_rev=0; p=s[0]=s[1]=NULL; }}*root[MAXN];void update(node *now){ if(!now) return; now->upv=now->s[0]?now->s[0]->upv:now->v; now->downv=now->s[1]?now->s[1]->downv:now->v; now->sum=1; if(now->s[0]) now->sum+=now->s[0]->sum-(now->v==now->s[0]->downv); if(now->s[1]) now->sum+=now->s[1]->sum-(now->v==now->s[1]->upv);}void print(node *now,int x){ if(!now) return; now->v=now->upv=now->downv=x; now->sum=1; now->lz=x;}void rev(node *now){ if(now) { swap(now->s[0],now->s[1]); swap(now->upv,now->downv); now->lz_rev^=1; }}void down(node *now){ if(now->lz_rev) { rev(now->s[0]); rev(now->s[1]); now->lz_rev=0; } if(now->lz) { print(now->s[0],now->lz); print(now->s[1],now->lz); now->lz=0; } update(now);}void link(node *f,node *x,bool d){ f->s[d]=x; if(x) x->p=f; update(f);}bool is_root(node *now){return !now->p||now!=now->p->s[0]&&now!=now->p->s[1];}void rotate(node *now,bool d){ node *x=now->s[d],*p=now->p; bool flag=is_root(now); link(now,x->s[d^1],d); link(x,now,d^1); if(flag) x->p=p; else link(p,x,now==p->s[1]);}stack<node*>s;void splay(node *now){ s.push(now); for(node *i=now;!is_root(i);i=i->p) s.push(i->p); while(!s.empty()) down(s.top()),s.pop(); while(!is_root(now)) { node *cur=now->p; bool d1=now==cur->s[1]; if(is_root(cur)) { rotate(cur,d1); return; } node *x=cur->p; bool d2=cur==x->s[1]; if(d1^d2) rotate(cur,d1),rotate(x,d2); else rotate(x,d2),rotate(cur,d1); }}void access(node *now){ node *x=NULL,*st=now; while(now) { splay(now); link(now,x,1); x=now; now=now->p; } splay(st);}void set_root(node *now){access(now),rev(now);}void extract(node *x,node *y){set_root(x),access(y);}void con(node *x,node *y){set_root(x),x->p=y;}int n,m;int main(){ ios::sync_with_stdio(0); cin>>n>>m; for(int i=1;i<=n;++i) { int a; cin>>a; root[i]=new node; root[i]->build(a); } for(int i=1;i<n;++i) { int a,b; cin>>a>>b; con(root[a],root[b]); } while(m--) { char op; int x,y,z; cin>>op; if(op=='C') { cin>>x>>y>>z; extract(root[x],root[y]); print(root[y],z); } else { cin>>x>>y; extract(root[x],root[y]); cout<<root[y]->sum<<endl; } } return 0;}