伸展樹（Splay Tree），也叫分裂樹，是一種二叉排序樹，它能在O(log n)內完成插入、查找和刪除操作。它由丹尼爾·斯立特Daniel Sleator 和 羅伯特·恩卓·塔揚Robert Endre Tarjan 在1985年發明的。
在伸展樹上的一般操作都基於伸展操作：假構想要對一個二叉查找樹執行一系列的查找操作，為了使整個查找時間更小，被查頻率高的那些條目就應當經常處於靠近樹根的位置。於是想到設計一個簡單方法， 在每次查找之後對樹進行重構，把被查找的條目搬移到離樹根近一些的地方。伸展樹應運而生。伸展樹是一種自調整形式的二叉查找樹，它會沿著從某個節點到樹根之間的路徑，通過一系列的旋轉把這個節點搬移到樹根去。
它的優勢在於不需要記錄用於平衡樹的冗餘信息。
基本介紹
- 中文名：伸展樹
- 外文名：Splay Tree
- 別名：分裂樹
- 類別：自平衡二叉查找樹
- 優勢：不需要記錄用於平衡樹的冗餘信息
- 學科：計算機
存在的意義,重構方法,支持的操作,伸展操作,查找操作,加入操作,刪除操作,合併操作,啟發式合併,劃分操作,其他操作,優勢,缺點,
存在的意義
假構想要對一個二叉查找樹執行一系列的查找操作。為了使整個查找時間更小，被查頻率高的那些條目就應當經常處於靠近樹根的位置。於是想到設計一個簡單方法， 在每次查找之後對樹進行重構，把被查找的條目搬移到離樹根近一些的地方。splay tree應運而生。splay tree是一種自調整形式的二叉查找樹，它會沿著從某個節點到樹根之間的路徑，通過一系列的旋轉把這個節點搬移到樹根去。
重構方法
先前，已經存在兩種重構方法：
1、單旋：在查找完位於節點x中的條目i之後，旋轉連結x和其父節點的邊。（除非x就是樹根）
2、搬移至樹根：在查找完位於節點x中的條目i之後，旋轉連結x和其父節點的邊，然後重複這個操作直至x成為樹根。
splay tree的重構方法和搬移至樹根的方法相似，它也會沿著查找路徑做自底向上的旋轉，將被查找條目移至樹根。但不同的是，它的旋轉是成對進行的，順序取決於查找路徑的結構。為了在節點x處對樹進行splay操作，我們需要重複下面的步驟，直至x成為樹根為止：
1、第一種情況：如果x的父節點p(x)是樹根，則旋轉連線x和p(x)的邊。（這種情況是最後一步）
2、第二種情況：如果p(x)不是樹根，而且x和p(x)本身都是左孩子或者都是右孩子，則先旋轉連線p(x)和x的祖父節點g(x)的邊，然後再旋轉連線x和p(x)的邊。
3、第三種情況：如果p(x)不是樹根，而且x是左孩子，p(x)是右孩子，或者相反，則先旋轉連線x和p(x)的邊，再旋轉連線x和新的p(x)的邊。
在節點x處進行splay操作的時間是和查找x所需的時間成比例的。splay操作不單是把x搬移到了樹根，而且還把查找路徑上的每個節點的深度都大致減掉了一半。
支持的操作
伸展操作
伸展操作Splay(x,S)是在保持伸展樹有序性的前提下，通過一系列旋轉將伸展樹S中的元素x調整至樹的根部。在調整的過程中，要分以下三種情況分別處理：
情況一：節點x的父節點y是根節點。這時，如果x是y的左孩子，我們進行一次Zig（右旋）操作；如果x是y的右孩子，則我們進行一次Zag（左旋）操作。經過旋轉，x成為二叉查找樹S的根節點，調整結束。即：如果當前結點父結點即為根結點，那么我們只需要進行一次簡單旋轉即可完成任務，我們稱這種旋轉為單旋轉。
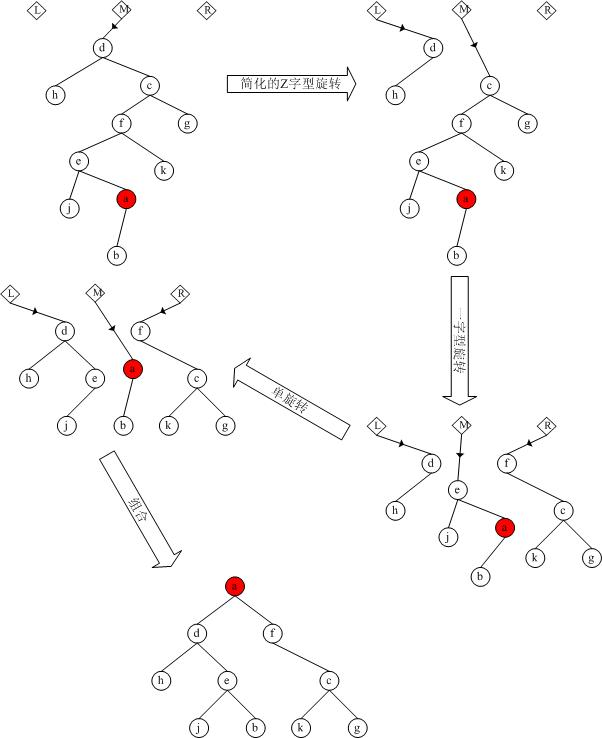
情況二：節點x的父節點y不是根節點，y的父節點為z，且x與y同時是各自父節點的左孩子或者同時是各自父節點的右孩子。這時，我們進行一次Zig-Zig操作或者Zag-Zag操作。即：設當前結點為X，X的父結點為Y，Y的父結點為Z，如果Y和X同為其父親的左孩子或右孩子，那么我們先旋轉Y，再旋轉X。我們稱這種旋轉為一字形旋轉。
情況三：節點x的父節點y不是根節點，y的父節點為z，x與y中一個是其父節點的左孩子而另一個是其父節點的右孩子。這時，我們進行一次Zig-Zag操作或者Zag-Zig操作。即：這時我們連續旋轉兩次X。我們稱這種旋轉為之字形旋轉。
如圖4所示，執行Splay(1,S)，我們將元素1調整到了伸展樹S的根部。再執行Splay(2,S)，如圖5所示，我們從直觀上可以看出在經過調整後，伸展樹比原來“平衡”了許多。而伸展操作的過程並不複雜，只需要根據情況進行旋轉就可以了，而三種旋轉都是由基本得左旋和右旋組成的，實現較為簡單。
查找操作
Find(x,S)：判斷元素x是否在伸展樹S表示的有序集中。
首先，與在二叉查找樹中的查找操作一樣，在伸展樹中查找元素x。如果x在樹中，則再執行Splay(x,S)調整伸展樹。
加入操作
Insert(x,S)：將元素x插入伸展樹S表示的有序集中。
首先，也與處理普通的二叉查找樹一樣，將x插入到伸展樹S中的相應位置上，再執行Splay(x,S)。
刪除操作
Delete(x,S)：將元素x從伸展樹S所表示的有序集中刪除。
首先，用在二叉查找樹中查找元素的方法找到x的位置。如果x沒有孩子或只有一個孩子，那么直接將x刪去，並通過Splay操作，將x節點的父節點調整
到伸展樹的根節點處。否則，則向下查找x的後繼y，用y替代x的位置，最後執行Splay(y,S)，將y調整為伸展樹的根。
合併操作
join(S1,S2)：將兩個伸展樹S1與S2合併成為一個伸展樹。其中S1的所有元素都小於S2的所有元素。首先，我們找到伸展樹S1中最大的一個元素x，再通過Splay(x,S1)將x調整到伸展樹S1的根。然後再將S2作為x節點的右子樹。這樣，就得到了新的伸展樹S。
啟發式合併
當S1和S2元素大小任意時，將規模小的伸展樹上的節點一一插入規模大的伸展樹，總時間複雜度O(Nlg^2N)。
劃分操作
Split(x,S)：以x為界，將伸展樹S分離為兩棵伸展樹S1和S2，其中S1中所有元素都小於x，S2中的所有元素都大於x。首先執行Find(x,S)，將元素x調整為伸展樹的根節點，則x的左子樹就是S1，而右子樹為S2。
其他操作
除了上面介紹的五種基本操作，伸展樹還支持求最大值、求最小值、求前趨、求後繼等多種操作，這些基本操作也都是建立在伸展操作的基礎上的。
通常來說，每進行一種操作後都會進行一次Splay操作，這樣可以保證每次操作的平攤時間複雜度是O(logn)。
優勢
- 可靠的性能——它的平均效率不輸於其他平衡樹。
- 存儲所需的記憶體少——伸展樹無需記錄額外的什麼值來維護樹的信息，相對於其他平衡樹，記憶體占用要小。
