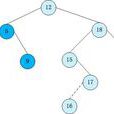
二叉搜尋樹

二叉搜尋樹

二叉查找樹（Binary Search Tree），（又：二叉搜尋樹，二叉排序樹）它或者是一棵空樹，或者是具有下列性質的二叉樹： 若它的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值； 若它的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值； 它的左、右子樹也分別為二叉排序樹。

基本介紹

  • 中文名：二叉搜尋樹
  • 外文名：Binary Search Tree
  • 學科：計算機
  • 分類：二叉樹
原理,算法實現,查找算法,插入算法,情況討論,

原理

二叉排序樹的查找過程和次優二叉樹類似，通常採取二叉鍊表作為二叉排序樹的存儲結構。中序遍歷二叉排序樹可得到一個關鍵字的有序序列，一個無序序列可以通過構造一棵二叉排序樹變成一個有序序列，構造樹的過程即為對無序序列進行排序的過程。每次插入的新的結點都是二叉排序樹上新的葉子結點，在進行插入操作時，不必移動其它結點，只需改動某個結點的指針，由空變為非空即可。搜尋,插入,刪除的複雜度等於樹高，O(log(n)).

算法實現

1 二叉排序樹的查找算法
2 在二叉排序樹插入結點的算法
3 在二叉排序樹刪除結點的算法
4 二叉排序樹性能分析

查找算法

在二叉排序樹b中查找x的過程為：
若b是空樹，則搜尋失敗，否則：
若x等於b的根結點的數據域之值，則查找成功；否則：
若x小於b的根結點的數據域之值，則搜尋左子樹；否則：
查找右子樹。
Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &*p){
//在根指針T所指二叉排序樹中遞歸地查找其關鍵字等於key的數據元素，若查找成功，
//則指針p指向該數據元素結點，並返回TRUE，否則指針指向查找路徑上訪問的最後
//一個結點並返回FALSE，指針f指向T的雙親，其初始調用值為NULL
if(!T){ p=f; return FALSE;} //查找不成功
else if EQ(key, T->data.key) {P=T; return TRUE;} //查找成功
else if LT(key,T->data.key)
return SearchBST(T->lchild, key, T, p); //在左子樹中繼續查找
else return SearchBST(T->rchild, key, T, p); //在右子樹中繼續查找
pascal語言實現
type
Link = ^tree;
Tree = record
D :longint;
Left :link;
Right :link;
End;
function search(n :longint;t :link):boolean;
Begin
If t^.d < n then begin
If t^.right = nil then exit(false) else exit(search(n,t^.right));
End;
If t^.d > n then begin
If t^.left = nil then exit(false) else exit(search(n,t^.left));
End;
Exit(true);
End;

插入算法

向一個二叉排序樹b中插入一個結點s的算法，過程為：
若b是空樹，則將s所指結點作為根結點插入，否則：
若s->data等於b的根結點的數據域之值，則返回，否則：
若s->data小於b的根結點的數據域之值，則把s所指結點插入到左子樹中，否則：
把s所指結點插入到右子樹中。
/*當二叉排序樹T中不存在關鍵字等於e.key的數據元素時，插入e並返回TRUE，否則返回FALSE*/
Status InsertBST(BiTree &T, ElemType e)
{
if(!SearchBST(T, e.key, NULL,p)
{
s=(BiTree *)malloc(sizeof(BiTNode));
s->data = e; s->lchild = s->rchild = NULL;
if(!p) T-s;
//被插結點*s為新的根結點
else if LT(e.key, p->data.key) p->lchld = s;
//被子插結點*s為左孩子
else ->rchild = s;
//被插結點*s為右孩子
return TRUE;
}
else
return FALSE;
//樹中已有關鍵字相同的結點，不再插入
}
pascal代碼:
procedure push(n :longint;var t:link);
Var P,q :link;
Begin
If t^.d < n then begin
If t^.right = nil then begin
New(p);
P^.d := n;
P^.right := nil;
P^.left := nil;
T^.right := p;
End else push(n,t^.right);
End else begin
If t^.left = nil then begin
New(p);
P^.d := n;
P^.right := nil;
P^.left := nil;
T^.left := p;
End else push(n,t^.left);
End;
End;

情況討論

在二叉排序樹刪去一個結點，分三種情況討論：
若*p結點為葉子結點，即PL(左子樹)和PR(右子樹)均為空樹。由於刪去葉子結點不破壞整棵樹的結構，則只需修改其雙親結點的指針即可。
若*p結點只有左子樹PL或右子樹PR，此時只要令PL或PR直接成為其雙親結點*f的左子樹或右子樹即可，作此修改也不破壞二叉排序樹的特性。
若*p結點的左子樹和右子樹均不空。在刪去*p之後，為保持其它元素之間的相對位置不變，可按中序遍歷保持有序進行調整，可以有兩種做法：其一是令*p的左子樹為*f的左子樹，*s為*f左子樹的最右下的結點，而*p的右子樹為*s的右子樹；其二是令*p的直接前驅（或直接後繼）替代*p，然後再從二叉排序樹中刪去它的直接前驅（或直接後繼）。在二叉排序樹上刪除一個結點的算法如下：
Status DeleteBST(BiTree &T, KeyType key){
//若二叉排序樹T中存在關鍵字等於key的數據元素時，則刪除該數據元素，並返回
//TRUE；否則返回FALSE
if(!T) return FALSE; //不存在關鍵字等於key的數據元素
else{
if(EQ(key, T->data.key)) {return Delete(T)}; 找到關鍵字等於key的數據元素
else if(LT(key, T->data.key)) return DeleteBST(T->lchild, key);
else return DeleteBST(T->rchild, key);
}
}
Status Delete(BiTree &p){
//從二叉排序樹中刪除結點p，並重接它的左或右子樹
if(!p->rchild){ //右子樹空則只需重接它的左子樹
q=p; p=p->lchild; free(q);
}
else if(!p->lchild){ //左子樹空只需重接它的右子樹
q=p; p=p->rchild; free(q);
}
else{ //左右子樹均不空
q=p;
s=p->lchild;
while(s->rchild){
q=s;
s=s->rchild
} //轉左，然後向右到盡頭
p->data = s->data; //s指向被刪結點的“前驅”
if(q!=p)
q->rchild = s->lchild; //重接*q的右子樹
else
q->lchild = s->lchild; //重接*q的左子樹
free(s);
}
return TRUE;
}

熱門詞條

聯絡我們