線性隨機系統即同時滿足線性系統和隨機控制系統特性的系統,它滿足線性系統的疊加性與均勻性,同時又受隨機因素影響。線性隨機系統分為連續線性隨機系統和離散線性隨機系統。
基本介紹
- 中文名:線性隨機系統
- 外文名:linear stochastic system
- 學科:控制科學與工程
- 類別:線性系統、隨機系統
- 分類:連續、離散
- 主要特性:能檢測性、能觀測性
基本概念
連續時間線性隨機系統
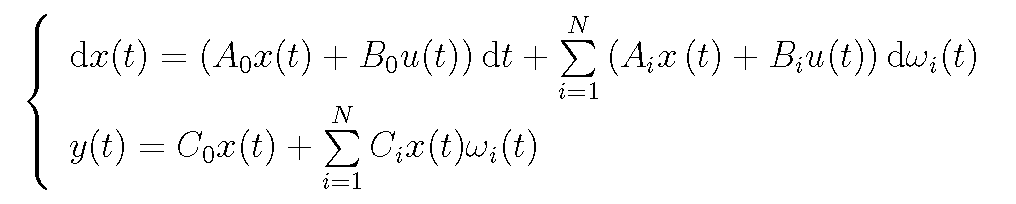
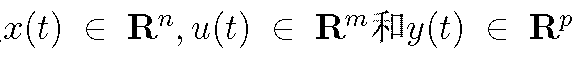
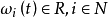
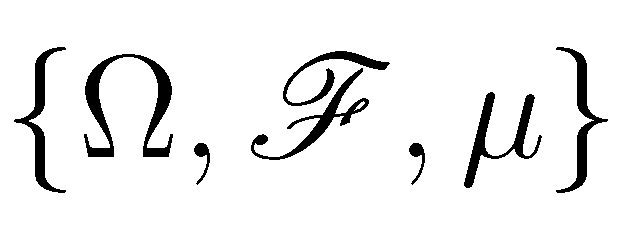
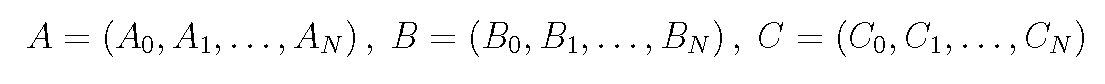
均方穩定性
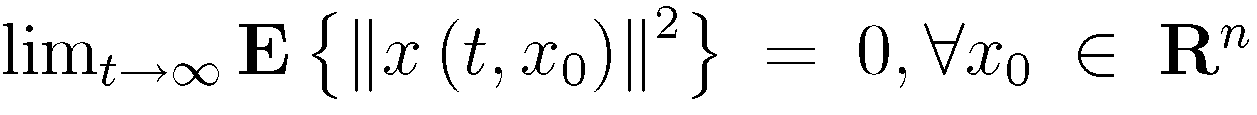
均方鎮定性

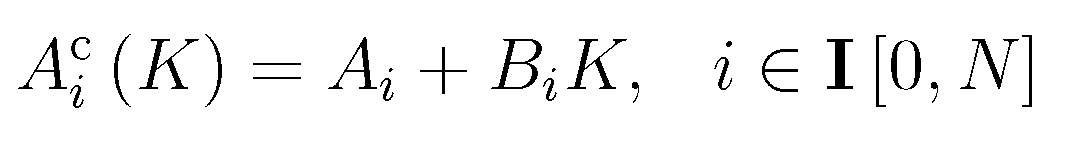
能檢測性
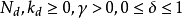
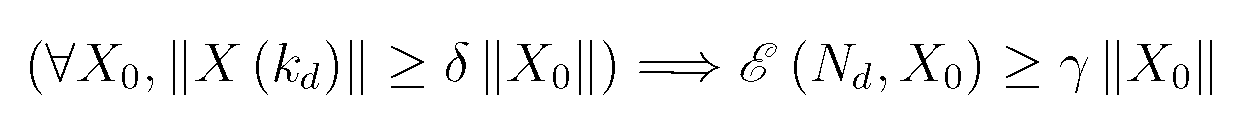
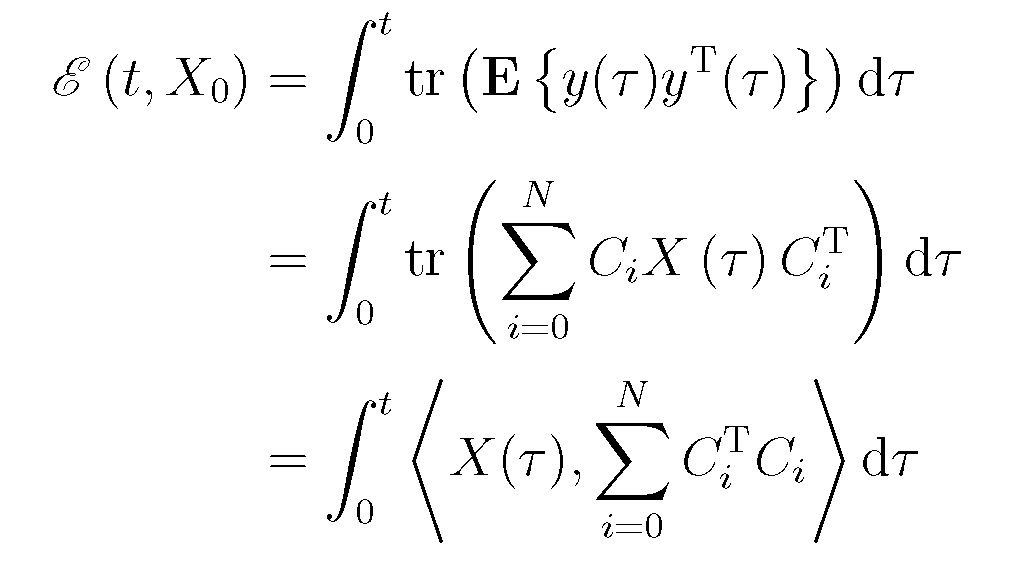
能觀測性
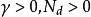
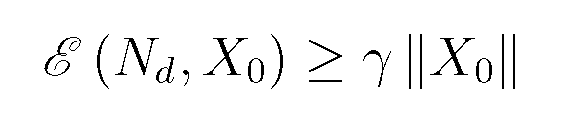
離散時間線性隨機系統
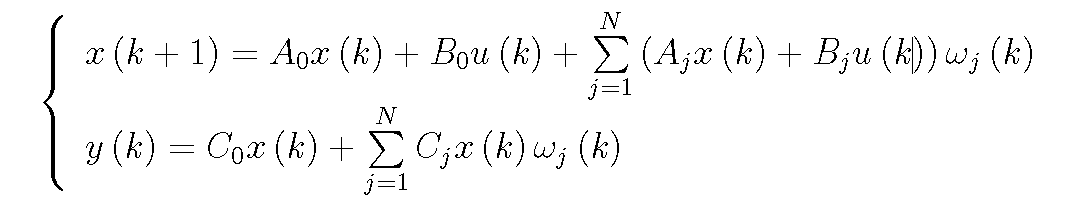
能檢測性
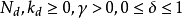
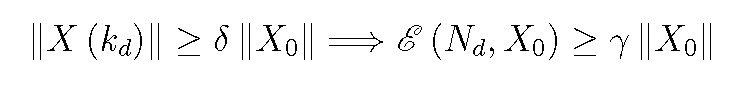
能觀測性
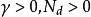
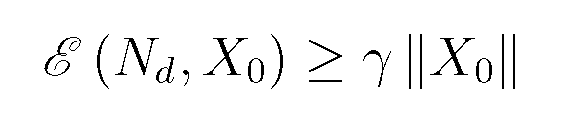
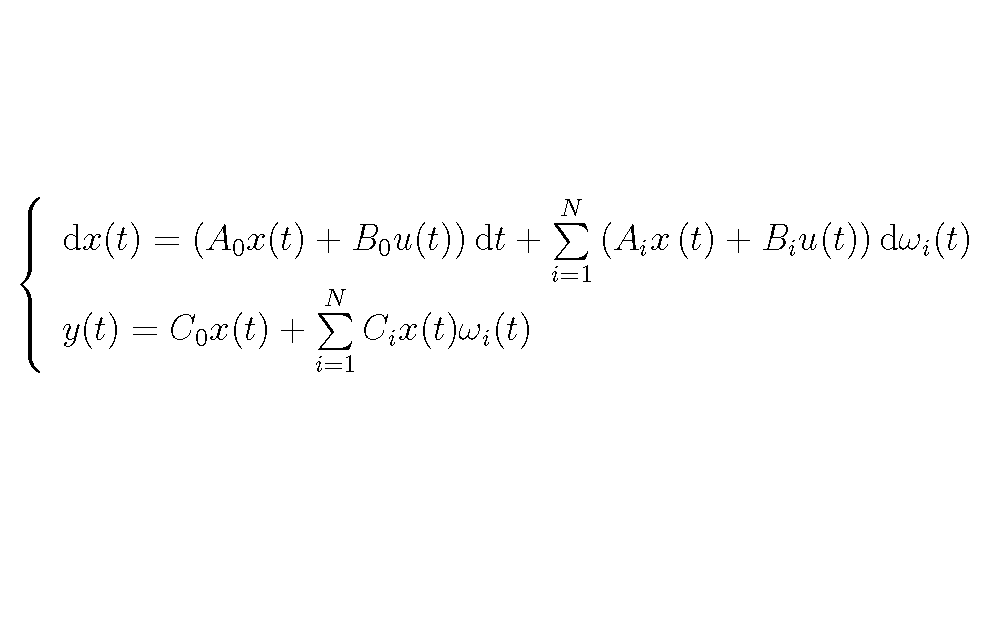
線性隨機系統即同時滿足線性系統和隨機控制系統特性的系統,它滿足線性系統的疊加性與均勻性,同時又受隨機因素影響。線性隨機系統分為連續線性隨機系統和離散線性隨機系統。
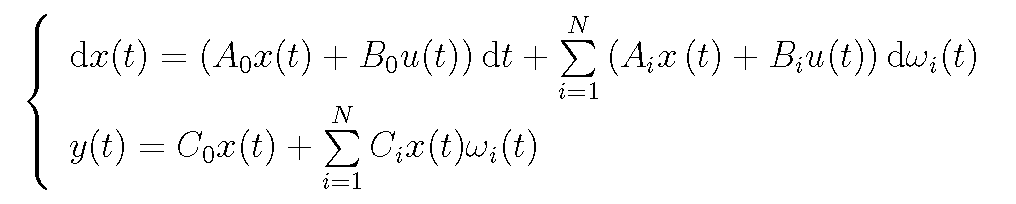
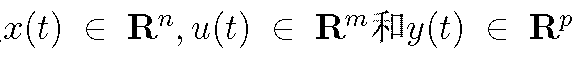
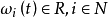
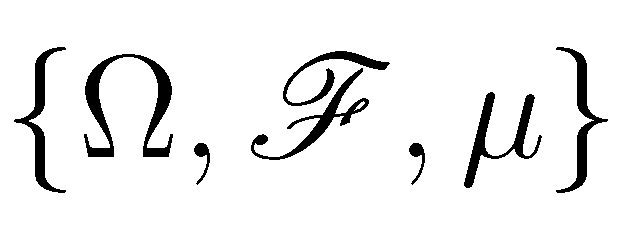
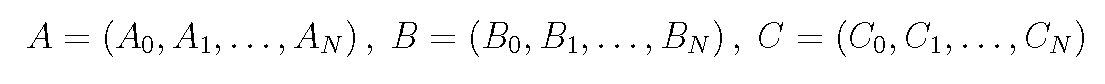
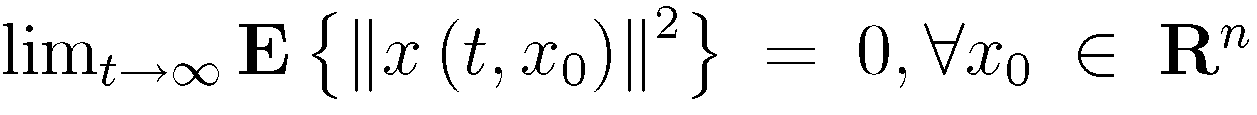

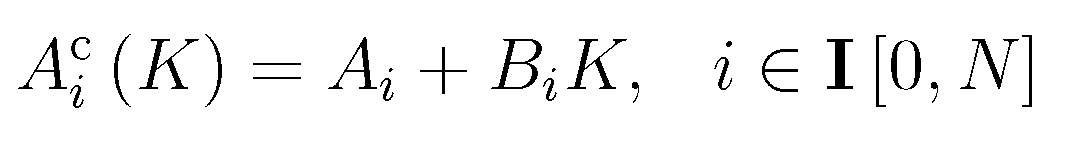
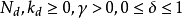
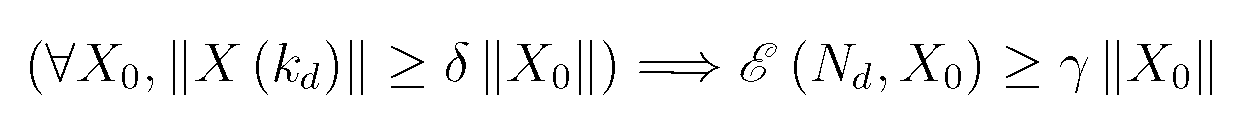
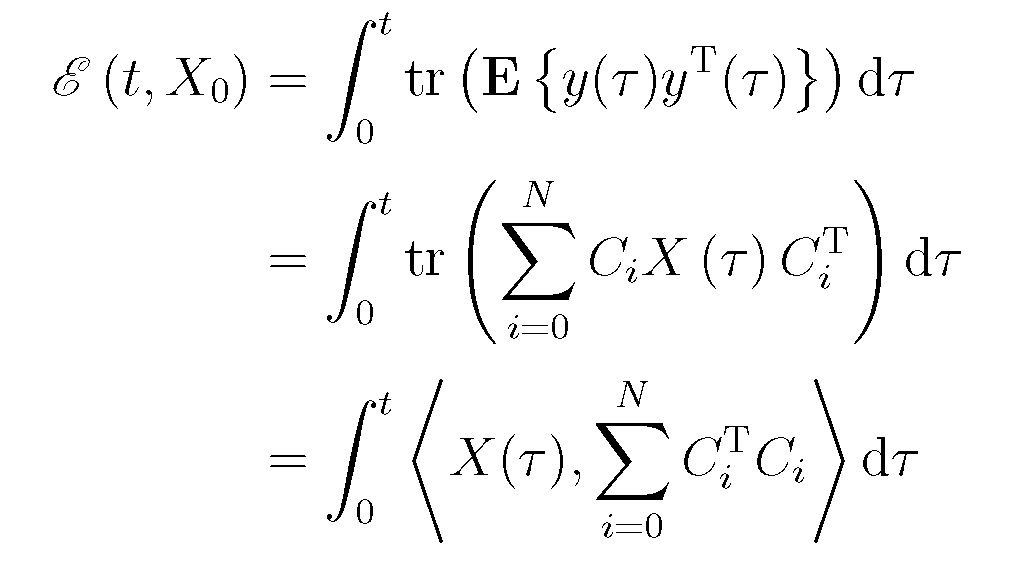
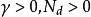
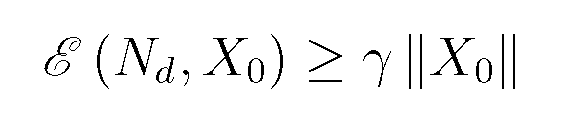
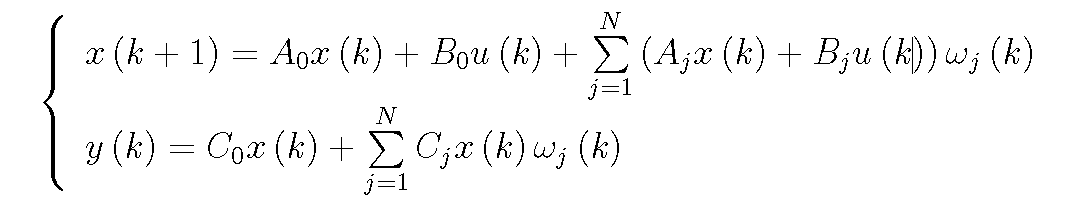
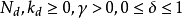
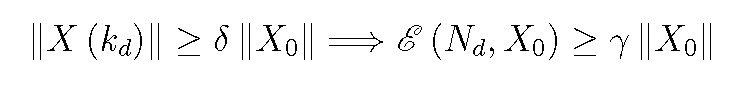
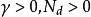
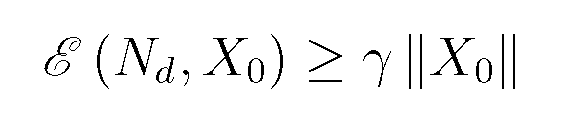
線性隨機系統即同時滿足線性系統和隨機控制系統特性的系統,它滿足線性系統的疊加性與均勻性,同時又受隨機因素影響。線性隨機系統分為連續線性隨機系統和離散線性隨機...
隨機控制系統受隨機因素影響的動態系統。通常用隨機微分方程或隨機差分方程來描述。...
本書是為工科院校自動控制、控制理論和系統工程等專業研究生編寫的隨機系統理論教材,內容包括隨機系統分析、系統的狀態估計、隨機最優控制、系統辨識與參數估計、自...
隨機系統控制的研究成果集中於對系統輸出變數本身的跟蹤,典型的例子是最小方差控制、線性二次型控制(LOG)、具有馬爾柯夫階躍參數系統的隨機控制,等等,控制目標是系統...
《隨機系統分析及套用》是由西北工業大學出版社出版圖書,作者是方洋旺。本書介紹了國內外控制理論及信號處理專家在隨機系統分析領域的最新研究成果。針對離散及連續...
動態系統一般分為確定性和隨機性兩類。一般地說,系統是由若干相互作用而各自具有相對獨立性的子系統構成,同時,系統作為一個整體又處在與環境的相互作用之中。相互...
《隨機系統最優控制》是2005年清華大學出版社出版的圖書,作者是方洋旺。本書全面介紹了原蘇聯及俄羅斯控制專家和其他專家以及作者在此領域的最新成果,詳細討論了隨機...
《系統與控制中的隨機方法》內容分為3大部分共7章。第1部分內容包括機率論基礎知識、統計量與抽樣分布、參數估計及貝葉斯推斷;第2部分內容是濾波和隨機線性系統的...
線性系統對隨機信號回響(response of lin-ear system to random signal)線性系統分析中的基本概念.對於穩定的線性非移變系統,如果輸人隨機過程是平穩的,則輸出隨機...
隨機控制理論是控制理論的一個分支。隨機控制理論通過控制器的最優設計來預測被控系統的隨機偏差量值的大小和極限,並使這種隨機偏差的量值達到最小。當隨機信號進入...
《結構隨機跳變系統最優控制理論》是關於結構隨機跳變系統最優控制理論與套用的一本著作。書中重點介紹了近十幾年國內外學者在此領域的最新研究成果,詳細討論了...
隨機最優控制(Stochastic optimal control)是指選擇控制變數,使隨機系統某個性能指標達到最優的控制。在隨機系統控制中,必須進行狀態估計。套用不同的狀態估計方法,會...
隨機系統是指該系統的輸入輸出或干擾存在隨機因素,或者系統本身具有某種不確定性。當前狀態的變化率不僅與當前時刻的狀態有關,而且也依賴於過去某時刻或某段時間的...
從這個結論可以看出m序列是一種“極差”的序列,它的線性複雜度太小,因而不能夠直接用來做流密碼系統的密鑰流序列。從這裡還可以看到僅僅靠Golomb的三個隨機性假設...
《生物系統的隨機動力學》是2009年科學出版社出版的圖書,作者是周天壽。...... 《生物系統的隨機動力學》是2009年科學出版社出版的圖書,作者是周天壽。...
《隨機信號與系統》主要討論隨機信號的基礎理論和分析方法。全書共分5章,包括機率論基礎,隨機信號的時、頻域特性,隨機信號通過線性系統的特性,隨機信號的相關實驗與...
隨機離散事件動態系統(stochastic discrete event dynamic system)簡稱隨機DEDS.按隨機規律進行狀態遷移的離散事件系統.諸如事件發生的種類和時刻服從隨機分布、狀態遷移...
《結構隨機跳變系統理論及其套用》是2007年科學出版社ISBN9787030188168出版的圖書,作者是吳森堂。...
