維里定理(英語:Virial theorem,又稱位力定理,均功定理)是描述穩定的多自由度體系的總動能和體系的總勢能時間平均之間的數學關係。
基本介紹
- 中文名:維里定理
- 外文名:Virial theorem
- 別稱:位力定理,均功定理
定義
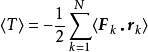
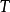

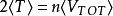
天體物理



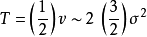
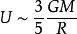

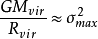
維里定理(英語:Virial theorem,又稱位力定理,均功定理)是描述穩定的多自由度體系的總動能和體系的總勢能時間平均之間的數學關係。
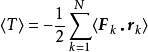
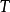

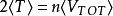



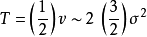
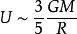

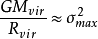
維里定理(英語:Virial theorem,又稱位力定理,均功定理)是描述穩定的多自由度體系的總動能和體系的總勢能時間平均之間的數學關係。...
關於位力定理的導出,可以將維里看作是系統慣量的時間導數,再進一步對維里求導得出,當然也需要證明,對穩定系統,慣量的二階時間導數平均值為0,過程也不算太麻煩。...
費曼(R.F.Feynman)-海爾曼(H.Hellma-nn)定理又稱費曼一海爾曼關係,發表於30年代後期。它套用極廣,既可用作理論分析,又可用於具體計算。凡用維里定理可以處理...
1.7.4 維里定理的某些簡化形式1.7.5 Hellmann-一Feynman定理1.8 表示理論1.8.1 態的表示1.8.2 算符的表示1.8.3 另一套量子力學的基本假設...
茲威基在1933年研究后髮座星系團時,率先使用維里定理推斷出其內部有看不見的物質,這就是現在所說的暗物質。他可以推斷在集團中星系的平均質量,而獲得的數值遠...
一方面我們可以根據速度彌散度,利用維里定理來估算團內每個星系的平均質量;另一方面,對星系團內部運動的研究又與探索星系團的穩定性問題密切相關。目前對這一問題有...
根據維里定理,當忽略自轉、磁場及湍流,只考慮引力勢能和熱能時,可得出如下星際雲自吸引塌縮條件: M>2.44×103M0. 式中M0=1.99×1033g,為太陽現質量。M為...
為深入理解共價鍵的本質,按雙原子分子的維里定理計算出2的〈T〉和〈V〉:又分子總能量E=〈T〉+〈V〉。如已知E 隨R 的改變的(dE/dR),則得:...
動能則為依據維里定理(Virial Theorem)( ),可以得到:如果我們假設質量和光度之間的關係是常數,即:我們可以觀察到消除質量M於是我們得到R和彌散速度的關係:...
他在研究Coma星系團的時候發現根據維里定理計算出的星系團的總質量要遠大於根據發光度計算出來的星系團質量,他推測星系團中存在著大量不發光的物質,並稱之為暗...
1933年,茲威基在研究后髮座星系團時,首先套用維里定理得出結論認為存在不可見的物質,即現在所說的暗物質,而這在當時並沒有引起重視。1934年,他和同事沃爾特·巴德...
檢查科馬星系群於1933年,是第一茲維基使用維里定理推斷看不見的物質的存在,這是他為鄧克爾質料 ' 暗物質 '。他內計算出星系的引力質量群集和得到的值的至少400...
造成這效應的高速度與星系團的重力相關,並可使用維里定理解釋;也就是觀測者所見星系團內星系的紅移和實際紅移不同。這效應會造成距離與紅移之間的關係哈勃定律的值...
2.3 劉維爾定理2.3.1 劉維爾定理證明2.3.2 維里定理2.3.3 平衡點和極限環2.3.4 彭伽勒回歸定理2.4 哈密頓-雅可比方程...
根據維里定理,這意味著核心溫度和壓力將增加。這會導致光度增加,所以 R136a1 要稍微比它形成時更明亮。R136a1 溫度已略有下降,恆星的外層已經膨脹,質量也損失...
2.2 能量均分定理和維里定理 2.3 熱力學公式 2.3.1 熱力學公式推導 2.3.2 化學平衡 2.4 非理想氣體物態方程 2.4.1 方程推導 2.4.2 邁爾集團...
他在研究Coma星系團的時候發現根據維里定理計算出的星系團的總質量要遠大於根據發光度計算出來的星系團質量,他推測星系團中存在著大量不發光的物質,並稱之為暗...
f. 維里定理和能量成分12. 模擬溶劑影響,使用:a. 有效片斷勢(EFP)b. 極化連續模型(PCM)c. 自恰反應場(SCRF)13. 產生Hondo,Meldf,Gamess-UK,Gaussian 9x...
一方面我們可以根據速度彌散度,利用維里定理來估算團內每個星系的平均質量;另一方面,對星系團內部運動的研究又與探索星系團的穩定性問題密切相關。天體系統;另一種...
1.4.4維里定理 習題1 參考文獻 第2章 原子結構 2.1類氫離子的SchrOdinger方程 2.1.1引言 2.1.2變數分離 2.1.3解方程 2.1.4方程的解 2.1.5R方程的...
4.1維里定理 4.2非理想流體的狀態方程 4.3庫侖電漿的狀態方程 第五章 任意流體的二體關聯 5.1非理想流體中的關聯 5.1.1任意分子勢體系的關聯理論 5.1.2...
2.2.3維里定理27 參考文獻27 第3章力場28 3.1勢函式29 3.2簡正模式30 3.2.1特徵運動30 3.2.2分子光譜31 3.2.3光譜與力常數31 3.3簡單體系的分子...
4-7 維里定理 220閱讀 習題 223閱讀 第五章 正則變換 225閱讀 5-1 為什麼要作正則變換 225閱讀 5-2 正則變換生成函式 227閱讀 5-3 正則變換中生成...
2.2.5 維里定理 2.3電子自旋 2.3.1 自旋波函式、空間波函式和全波函式 2.3.2全同粒子和斯萊特行列式 2.3.3 電子自旋與物質的磁性 2.4原子光譜與原子光...
