定義
英文名稱:adiabatic invariant
在電漿物理學中,絕熱不變數是指在一個緩慢變化的系統中,若並不具有完全周期性運動的運動積分仍然為常數,則該運動積分可以稱為絕熱不變數,又稱浸漸不變數,或緩漸不變數。此處系統的變化需要比運動周期慢。
基本介紹
- 中文名:絕熱不變數
- 外文名:adiabatic invariant
- 學科:電漿物理學
- 參考資料:杜世剛.電漿物理
背景
相關量
μ
J
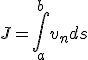
定義
英文名稱:adiabatic invariant
在電漿物理學中,絕熱不變數是指在一個緩慢變化的系統中,若並不具有完全周期性運動的運動積分仍然為常數,則該運動積分可以稱為絕熱不變數,又稱浸漸不變數,或緩漸不變數。此處系統的變化需要比運動周期慢。
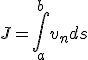
定義英文名稱:adiabatic invariant在電漿物理學中,絕熱不變數是指在一個緩慢變化的系統中,若並不具有完全周期性運動的運動積分仍然為常數,則該運動積分可以稱為...
《力學系統的對稱性與不變數》是1999年科學出版社出版的圖書,作者是趙躍宇,梅鳳翔。...
[24] 羅紹凱.Lagrange系統一類新型的非Noether絕熱不變數——Lutzky型絕熱不變數.物理學報,2007,56(10):5580-5584 SCI收錄,EI收錄,SCI引用...
《磁層粒子動力學》的內容包括帶電粒子在地磁場中的運動區、運動軌道、漂移運動的小擾動理論及其絕熱不變數等,並根據磁層不同區域內的電磁場特徵,將磁層分成近...
在1912年至1933年這段時期中埃倫費斯特的最重要的成就是絕熱不變數,他在量子物理學包括相變理論和埃倫費斯特理論做出了傑出貢獻。中文名 保羅·埃倫費斯特 外文名 ...
[1] 參考資料 1. 固體熱力學中的絕熱不變數和開爾文公式 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:8次歷史版本 最近更新: 創建者:心情fj猜...
緒論 相空間量子化的早期理論與絕熱不變數第1章 普朗克創世量子論的歷史回顧和普朗克公式的三種推導第2章 發展Dirac符號法的有序算符內的積分技術(IWOP技術)...
粒子軌道理論的另一個重要內容是浸漸不變數(曾稱絕熱不變數)。當帶電粒子在隨空間或時間緩慢變化的磁場中運動時,在一級近似理論中,存在著可視為常量的浸漸不...
正則變換§46 劉維爾定理§47 哈密頓一雅可比方程§48 分離變數§49 絕熱不變數§50 正則變數§51 絕熱不變數守恆精確性§52 條件周期運動朗道撰寫的第一版序...
對於磁場隨時間和空間的變化不是很劇烈的情況,在不均勻磁場中帶電粒子的運動,遵從磁矩守恆的規律,帶電粒子的磁矩(見絕熱不變數)。設在圖2系統的中部有一帶電...
105絕熱不變數和粒子漂移 I06電離層――磁層藕合 I07電離層電流 I08沿磁場的電位降 109磁層粒子進入地球大氣層的損失 10I0結語 參考讀物 習題 第十一章 脈動...
4.2.4絕熱不變數 4.3太陽能量粒子的發生和加速 4.4太陽能量粒子的傳播 4.4.1太陽粒子在日冕內的傳播 4.4.2 太陽能量粒子在行星際空間的傳播 4.5太陽宇宙線...
5.6 廣義Birkhoff系統對稱性攝動與絕熱不變數 5.6.1 廣義Birkhoff系統的攝動 5.6.2 廣義Birkhoff系統的絕熱不變數 5.7 廣義Birkhoff系統的積分不變數 5.7....
9.1.4 絕熱不變數和Hannay角 546 9.2 解題方法指導 547 9.3 習題解答 549 參考書目 594 [1] 參考資料 1. 理論力學學習指導與習題解析(理科用)(第二版) .京...
1.2 介觀量子電路中的絕熱不變數 1.3 由法拉第定理決定的介觀電路的數-相量子化方案與相算符的表示 第2章 狄拉克符號法知識補遺:量子力學表象理論的發展和IWOP...
1.4.12 對稱性攝動與絕熱不變數的研究1.4.13 動力學逆問題1.4.14 非完整系統動力學研究1.4.15 Birkhoff系統動力學研究1.4.16 約束系統幾何動力學研究...
8.2 非線性量子演化的絕熱條件與絕熱不變數8.3 半經典極限和絕熱極限的可交換性問題參考文獻第9章 Berry相9.1 非絕熱幾何相與經典Hannay角...
對於磁場隨時間和空間的變化不是很劇烈的情況,在不均勻磁場中帶電粒子的運動,遵從磁矩守恆的規律,帶電粒子的磁矩(見絕熱不變數)。設在圖2系統的中部有一帶電...
9.1.4 絕熱不變數和Hanndy角9.2 解題方法指導9.3 習題解答參考書目·收起全部<<參考資料 1. 理論力學學習指導與習題解析 .豆瓣[引用日期2019-04-04] ...
