基本介紹
- 中文名:組合總數
- 外文名:total number of combinations
- 所屬學科:數學
- 所屬問題:排列組合
基本介紹


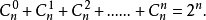
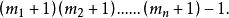
例題解析

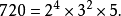
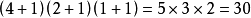

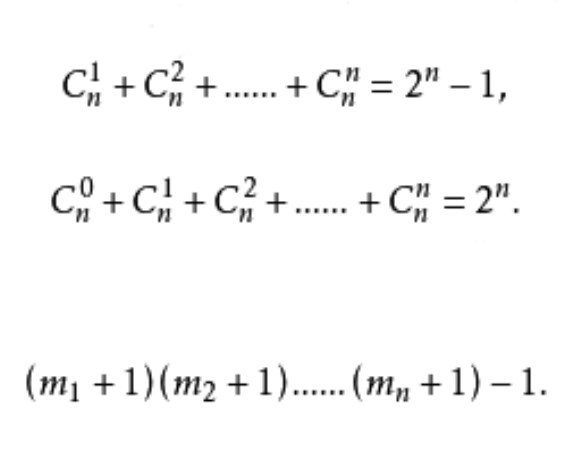


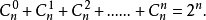
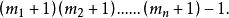

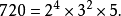
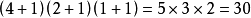

組合總數(total number of combinations)是一個正整數,指從n個不同元素里每次取出0個,1個,2個,…,n個不同元素的所有組合數的總和,即Cºn+C¹n+C²n...
組合(combination)是一個數學名詞。一般地,從n個不同的元素中,任取m(m≤n)個元素為一組,叫作從n個不同元素中取出m個元素的一個組合。我們把有關求組合的...
組合數公式是指從n個不同元素中,任取m(m≤n)個元素並成一組,叫做從n個不同元素中取出m個元素的一個組合;從n個不同元素中取出m(m≤n)個元素的所有組合...
排列總數(total number of permutations)是指從n個不同元素里每次取出1個,2個,... n個不同元素的所有排列數的總和,n元集合元素的排列總數等於它的非空有序子...
排列組合是組合學最基本的概念。所謂排列,就是指從給定個數的元素中取出指定個數的元素進行排序。組合則是指從給定個數的元素中僅僅取出指定個數的元素,不考慮...
重複組合(combination with repetition)是一種特殊的組合,從n個不同元素中可重複地選取m個元素,不管其順序合成一組,稱為從n個元素中取m個元素的可重複組合。兩...
組合運算是數學術語。...... 組合運算是數學術語。往往寫成Cxy C是指combination,Cxy是指從x個...從理解上來說,從n各裡面取出m個進行排列的取法總數,就等於先從...
產品組合的長度是指產品組合中所有產品線的產品項目總數。每一條產品線內的產品項目數量,稱為該產品線的長度。如果具有多條產品線,可將所有產品線的長度加起來,...
產品組合(或產品搭配)是指一個企業提供給市場的全部產品線和產品項目。產品組合,也稱"產品的各色品種集合(product assortment)",是指一個企業在一定時期內生產經營...
媒體組合是廣告活動中選擇媒體大類、具體媒體和投放手段的決策,首先,考慮H標客群接觸媒體的習慣、產品特點、信息特點和媒體成本等因素,在報刊、電視、網際網路、直郵等...
在數量型或價格型工具運用之爭中,有著很豐富的歷史背景和具體的政策內涵,不可形上學地貼以“孰優孰劣”的標籤。實際上,貨幣政策經常體現為組合形式,既包括...
組合最最佳化又稱組合規劃,是在給定有限集的所有具備某些特性的子集中,按某種目標找出一個最優子集的一類數學規劃。初期,它所研究的問題,如廣播網的設計、旅遊路線...
一不管甲乙的限制條件,即30人中選10人;二排除甲乙都參加的排法數;則總數為一...排列與組合全集(精講)圓排列 一、定義:有一組元素,將其排成一個圓,這種排列...
所謂產品組合的深度,是指產品大類中每種產品有多少花色品種規格。例如,寶潔公司的浪峰牌牙膏,假設有三種規格和兩種配方,由浪峰牌牙膏的深度為6。用品牌數除各種...
(組合建築形式)編輯 鎖定 本詞條由“科普中國”百科科學詞條編寫與套用工作項目...四合院建築之雅致,結構之巧,數量之眾多,當推北京為最。北京的四合院,大大小小,...
預算控制法是西方企業流行使用的方法,它通過人工成本預算控制人員數量,而不是對...因此,人力資源管理最重要的是如何運用有限的資本投入獲得最佳的崗位和人數的組合,...
排列數指的是從n個不同元素中任取r(r≦n)個元素排成一列(考慮元素先後出現次序)稱此為一個排列,此種排列的總數即為排列數,即叫做從n個不同元素中取出r個...
