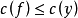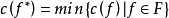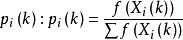在有限個可行解的集合中找出最優解的一類最佳化問題稱為組合最最佳化問題，它是運籌學中的一個重要分支。所研究的問題涉及信息技術、經濟管理、工業工程、交通運輸、通訊網路等諸多領域。組合最佳化算法(optimal combination algorithm)是一類在離散狀態下求極值的問題。
基本介紹
- 中文名：組合最佳化算法
- 外文名：optimal combination algorithm
- 學科：數學，計算機科學
- 類型：最佳化問題算法
- 基本算法：多項式時間算法
- 套用：裝箱、聚類問題等
組合最佳化問題,概念,數學定義,組合最佳化算法,多項式時間算法,近似算法,啟發式算法,遺傳算法,套用,
組合最佳化問題
概念
組合最佳化（或稱為離散最佳化）是一門古老而又年輕的學科，著名數學家Fermat，Euler等都為其形成和發展作出過重要貢獻二十世紀後半葉。伴隨著工業科技革命和現代管理科學的發展，特別是計算機技術的突飛猛進和在各行業的廣泛套用，組合最佳化已壯大成為運籌學的一個獨立分支。一些數百年前數學家們偶然想到的問題和方法，已在網路通信、物流管理、交通規劃等行業發揮了重要的作用，這是他們當時所不曾想到的。這從另一方面寓示了這學科的巨大前景。
組合（最）最佳化問題是最最佳化問題的一類。最最佳化問題似乎自然地分成兩類：一類是連續變數的問題，另一類是離散變數的問題。具有離散變數的問題，我們稱它為組合的。在連續變數的問題里，一般地是求一組實數，或者一個函式；在組合問題里，是從一個無限集或者可數無限集裡尋找一個對象——典型地是一個整數，一個集合，一個排列，或者一個圖。一般地，這兩類問題有相當不同的特色，並且求解它們的方法也是很不同的。對於具有離散變數的問題，從有限個解中尋找最優解的問題就是組合最最佳化問題。
數學定義
設F是有限集，c是F到R(實數集)的映射，即C是定義在F上的一個函式。求f∈F，使得對於任意的y∈F，有
一個組合最最佳化問題可用二元組(F，c)表示，其中F表示可行解區域，F中的任何一個元素稱為該問題的可行解，c表示目標函式。滿足
的可行解，f*稱為該問題的最優解。
組合最佳化算法
組合最佳化算法(optimal combination algorithm)一類在離散狀態下求極值的問題。把某種離散對象按某個確定的約束條件進行安排，當已知合乎這種約束條件的特定安排存在時，尋求這種特定安排在某個最佳化準則下的極大解或極小解的間題。組合最最佳化的理論基礎含線性規劃、非線性規劃、整數規劃、動態規劃、擬陣論和網路分析等。組合最最佳化技術提供了一個快速尋求極大解或極小解的方法。
多項式時間算法
組合最最佳化的特點是可行解集合為有限點集。只要將有限個點逐一比較目標值的大小，該問題最優解就一定可以得到。但是枚舉是以時間為代價的，有的枚舉時間還可以接受，有的則不能接受。設問題的規模為n，如果存在一個多項式p(n)，使得算法最多執行p(n)個基本步驟便可得到解答，則這種算法稱為多項式時間算法。
多少年來，人們試圖尋找解答各種組合問題的多項式時聞算法，這種研究工作在一些問題上已取得成功，其中包括最短路問題、最小支撐樹問題、網路最大流問題、最小費用流以及運輸問題等等。本文研究的無容量限制的帶固定費用的最小費用流問題及帶費用約束的緊急運輸問題也都找到了多項式時間算法。
隨著實踐的發展，出現了越來越多的組合最佳化問題都很難找到求最優解的多項式時間算法。經過幾代數學家的努力，他們研究整理了一類難以求解的組合最佳化問題，迄今為止還沒有一個能我到最優解的多項式時間算法。例如，最大團問題，TSP問題，點覆蓋問題，3-SAP問題等等都屬於這一類問題。
這一類組合最佳化問題歸為所謂的NP-hard問題。受人類認識能力的限制，目前人們只能假設這一類難解的組合最佳化問題不存在求最優解的多項式時間算法。正因為一些組合最佳化問題還沒有找到求最優解的多項式時間算法，而這些組合最佳化問題又有非常強的實際套用背景，人們不得不嘗試著為這些問題設計近似算法(Approximate Algorithm)、啟發式算法(Heuristic Algorithm)、或者遺傳算法(Genetic Algorithm)等。
近似算法
我們將尋找能在較短時間（多項式時間）內得到接近予最優解的算法，稱之為近似算法(approximation
algorithm)。衡量近似算法的優劣可從兩個方面來看，一是算法的時間複雜性，二是它得到的解值與最優解值的接近程度。
algorithm)。衡量近似算法的優劣可從兩個方面來看，一是算法的時間複雜性，二是它得到的解值與最優解值的接近程度。
近似算法能夠保證計算結果與最優結果相比較的差別不超過某一常數α，且α一般較小，但是算法比較複雜，在計算機上編程時比較困難。
啟發式算法
啟發式算法通常很簡單，很容易在計算機上實現，一般情況下也能夠保證計算結果同最優結果差別不超過某一常數α，但是相對於近似算法要大。也有一些啟發式算法無法保證解的近似度，但計算結果通常都比較理想。常見的啟發式算法有NF(Next Fit)近似算法，FF(First Fit)近似算法．FFD(First Fit Decreasing)近似算法，BF(best Fit)，BFD(Best Fit Deceasing)近似算法等。
遺傳算法
遺傳算法簡稱GA，是一種借鑑生物界自然選擇和自然遺傳機制的高度並行、隨機、自適應的搜尋方法，由於遺傳算法的尋優過程是從大量的點構成的種群開始平行進行、逐步最佳化，避免了局部最佳化結果的產生，並且，遺傳算法不要求函式滿足可導性質，因此遺傳算法常用來解決傳統搜尋方法解決不了或很難解決的問題，計算結果與最優結果差別一般也很小，但是計算時間相對較長，而且無法從理論上保證計算結果的好壞。
與其他啟發式搜尋方法一樣，遺傳算法在形式上是一種疊代方法，它從一組解（ 群體）出發，模擬生物體的進化機制，採用複製、交叉、變異等遺傳操作，在繼承原有優良基因的基礎上，生成具有更好性能指標的下一代解的群體，不斷疊代，直到搜尋到最優解或滿意解為止。用遺傳算法解決組合最佳化問題的一般方法：
（1）確定群體規模I（整數）及遺傳操作的代數（整數）。初試代數k = 1，使用隨機方法或其他方法產生I 個可能解Xi （ 1<=i<=n，k = 1）組成初始解群。
（2）對於群體中每一個個體Xi （ k），計算其適應度 f（Xi （ k））。
（3）若whiie（！結束條件）
對於群體中每一個體Xi（ k ），計算其生存機率
根據生存機率Pi （ k），在群體中選擇父體執行遺傳操作，包括複製、交叉、變異，得到一個新的解群體，此時k = k + 1，轉（2）步。
（4）滿足條件，結束操作。
遺傳算法解決問題的第一步是確定編碼方案，而編碼方案的選取在很大程度上依賴於問題的性質及遺傳運算元的設計。組合最佳化問題都具有不同程度的約束條件，如TSP問題要求每個城市只能經過一次等，那么在編碼方案和遺傳運算元的設計上就有了一些特殊的要求。因此，在求解組合最佳化問題算法的具體實現過程中，主要工作包括確定編碼方案和設計遺傳運算元（交叉、變異等）。
套用
典型的組合最佳化問題有：
旅行商問題（Traveling Salesman Problem－TSP）；
加工調度問題（Scheduling Problem，如Flow-Shop，Job-Shop）；
0-1背包問題（Knapsack Problem）；
裝箱問題（Bin Packing Problem）；
圖著色問題（Graph Coloring Problem）；
聚類問題（Clustering Problem）等。
這些問題描述非常簡單，並且有很強的工程代表性，但最最佳化求解很困難，其主要原因是求解這些問題的算法需要極長的運行時間與極大的存儲空間，以致根本不可能在現有計算機上實現，即所謂的“組合爆炸”。正是這些問題的代表性和複雜性激起了人們對組合最佳化理論與算法的研究興趣。
