基本介紹
- 中文名:純超越擴張
- 外文名:purely transcendental extension
- 適用範圍:數理科學
定義



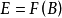
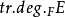
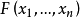


超越擴域
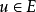
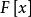
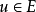





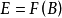
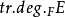
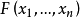


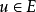
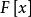
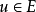

純超越擴張是一類重要的超越擴張。對於E的一個子集B,如果B在F上是代數無關的且E是F(B) 的代數擴域,那么B稱為E在F上的一個超越基(transcendentalbasis)。...
純量擴張(scalar extension)是常用的代數基域擴張,它對域上中心單代數結構的研究有重要作用。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F...
1 簡介 2 定義 3 抽象代數 4 域擴張 5 純超越擴張 代數擴張簡介 編輯 在抽象代數中,一個域擴張(通常記作)被稱作代數擴張,若且唯若每個的元素都是在...
正則擴張純超越擴張 編輯 純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越擴張,K為F的純超越擴域。此時,K與F...
純不可分擴張(purely inseparable extension )是一種重要的代數擴張。設K/F是代數擴張,若K中每個元均為F上的不可分元,則稱這個擴張為純不可分擴張。...
,如果L中元素要么屬於K,要么是K上的超越元,則稱L是K的純超越擴張。一個單擴張如果由添加代數元生成則是有限擴張,如果由添加超越元生成則是純超越擴張 [2] ...
有理函式域(rational function field)是一種重要的純超越擴張。純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越...
它當然是最簡單的代數簇。它可以等價地定義為代數閉域k上的代數簇X,X的有理函式域k(X)同構於域k的有限生成純超越擴張。 [1] ...
呂洛特定理(Liiroth theorem)關於單純超越擴張中間域的一條重要定理.若K=F(二)是域F的一個單超越擴域,E是其中間域且E並F,則必存在F上超越元t,使E=F(t...
全純域是刻畫自然邊界的域。C中的域Ω稱為全純域,如果不存在比Ω更大的域...,如果K的每個元都是F上的代數元,則稱K/F是代數擴張,否則稱K/F為超越擴張...
它深刻地刻畫了(相對)阿貝爾擴張。 [1] 代數元(algebraic element)是域論的...若這樣的多項式不存在,則α稱為F上的超越元。若α是F上的代數元,F[x]中以...
代數擴張是一類重要的域擴張。設E是F的擴域,若E中元皆為F上的代數元,則稱此域擴張為代數擴張,E稱為F的代數擴域,否則稱為超越擴張,而E稱為F的超越擴域。...
分裂域和正規擴張、可離擴張與單純性(包括跡與範數)、有限域、超越擴張等;在Galois理論部分,首先證明了Galois基本定理,然後進一步介紹了根式擴張與解方程、尺規作圖...
