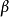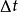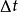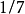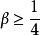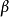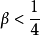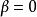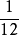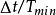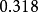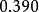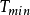紐馬克-β法是一種將線性加速度方法普遍化的方法。紐馬克方法可認為是概括了平均常加速度和線性加速度算法的一種廣義算法。紐馬克方法有擬靜力增量方程形式和不同類型的擬靜力全量方程形式。
基本介紹
- 中文名:紐馬克-β法
- 外文名:NewMark-β method
- 定義:將線性加速度方法普遍化的方法
- 套用學科:力學術語
- 範疇:數理科學
- 同類:威爾遜-θ法
概念,基本原理,
概念
紐馬克-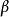 法是一種將線性加速度方法普遍化的方法。紐馬克-
法是一種將線性加速度方法普遍化的方法。紐馬克-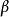 法可認為是概括了平均常加速度和線性加速度算法的一種廣義算法。紐馬克-
法可認為是概括了平均常加速度和線性加速度算法的一種廣義算法。紐馬克-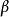 法有擬靜力增量方程形式和不同類型的擬靜力全量方程形式。在有限元動態分析中最常用的有中心差分法、紐馬克-
法有擬靜力增量方程形式和不同類型的擬靜力全量方程形式。在有限元動態分析中最常用的有中心差分法、紐馬克-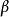 法(Newmark)和威爾遜-θ法。
法(Newmark)和威爾遜-θ法。
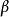
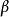
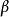
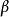
基本原理
紐馬克法是對線性加速度假定做了修正,在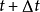 時刻的速度和位移表達式中引入兩個參數
時刻的速度和位移表達式中引入兩個參數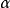 、
、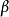 ,得紐馬克法的兩個基本方程:
,得紐馬克法的兩個基本方程:
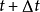
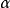
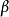
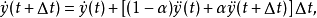
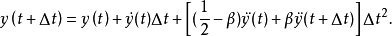
若在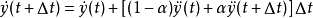 和
和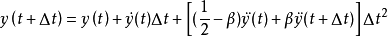 兩個式子中令
兩個式子中令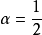 ,只保留參數
,只保留參數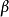 ,即為紐馬克-
,即為紐馬克-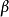 法。
法。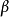 值常取為
值常取為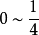 ;令
;令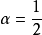 ,
,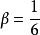 ,這就相當於加速度在
,這就相當於加速度在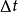 時段內線性變化,即威爾遜-
時段內線性變化,即威爾遜-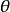 法中
法中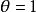 的情況;若令
的情況;若令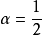 ,
,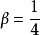 ,這相當於加速度在
,這相當於加速度在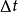 內為常量,其值為
內為常量,其值為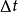 兩端加速度的平均值,即為平均加速度法。
兩端加速度的平均值,即為平均加速度法。
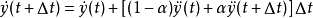
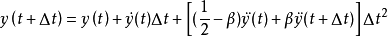
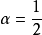
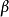
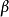
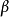
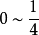
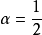
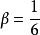
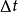
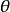
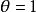
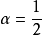
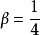
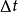
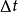
由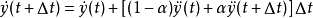 和
和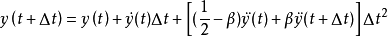 兩個式子,可得:
兩個式子,可得:
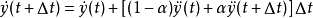
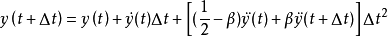
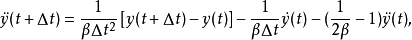
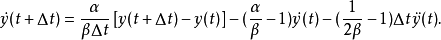
將上面兩個式子代入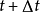 時刻的動力方程,經整理後得:
時刻的動力方程,經整理後得:
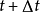
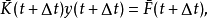
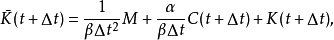
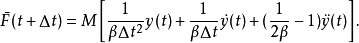
紐馬克-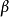 法的計算精度取決於時間步長
法的計算精度取決於時間步長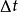 的大小。而時間步長的確定必須考慮荷載變化情況和系統自振周期的長短。為了保證感興趣的高頻分量的貢獻,通常要求
的大小。而時間步長的確定必須考慮荷載變化情況和系統自振周期的長短。為了保證感興趣的高頻分量的貢獻,通常要求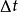 小於對回響有重要影響的最小結構自振周期的
小於對回響有重要影響的最小結構自振周期的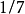 。穩定性研究還表明:當
。穩定性研究還表明:當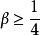 時,紐馬克-
時,紐馬克-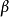 法是無條件穩定的;
法是無條件穩定的;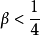 時,則是有條件穩定的,其穩定性條件為:對於
時,則是有條件穩定的,其穩定性條件為:對於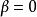 ,
,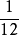 和
和 這三種情況,
這三種情況,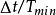 必須分別小於
必須分別小於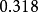 ,
,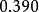 和
和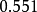 ,其中
,其中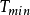 為結構的最小自振周期。
為結構的最小自振周期。