威爾遜-θ法是線上性加速度法的一種拓展,其基本思路和實現方法是在時間段[t,t+θ△t]內線性變化,首先計算ti+θ△t時刻的運動,其中θ>1,然後通過內插得到時刻ti+△t的運動。可以證明當θ≥1.37時,威爾遜-θ法是無條件穩定的。
基本介紹
- 中文名:威爾遜-θ法
- 外文名:Wilson-θ
- 領域:力學
- 性質:θ≥1.37時無條件穩定
- 地位:線性加速度法的一種拓展
簡介,推導過程,威爾遜-θ法計算步驟,
簡介
威爾遜-θ法是線上性加速度法的一種拓展,其基本思路和實現方法是在時間段[t,t+θ△t]內線性變化,首先計算ti+θ△t時刻的運動,其中θ>1,然後通過內插得到時刻ti+△t的運動。可以證明當θ≥1.37時,威爾遜-θ法時無條件穩定的。
推導過程

其中τ為局部時間坐標,坐標原點在ti。對上式積分,得到速度,位移為:
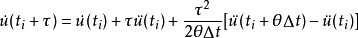

當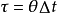 時,由上述兩式得:
時,由上述兩式得:
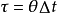
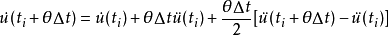
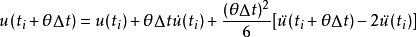
在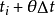 時刻,體系的運動應滿足運動方程:
時刻,體系的運動應滿足運動方程:
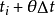
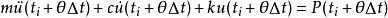
其中外載荷向量
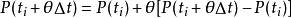
因此得到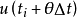 的方程:
的方程:
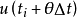
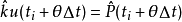
以及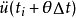
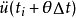
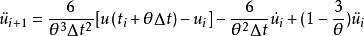
令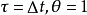 ,我們得到
,我們得到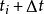 時刻的速度,位移為:
時刻的速度,位移為:
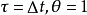
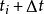
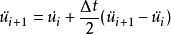
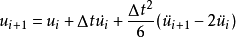
上面三個式子構成了單自由度體系動力反應分析的威爾遜-θ法計算公式。
威爾遜-θ法計算步驟
當i=0時,第0段:
確定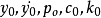 ,因此計算出
,因此計算出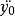 以及等效剛度、荷載矢量、等效剛度,至此,第0段的反應已經計算完畢,已經有了初始量,可以進入疊代計算。
以及等效剛度、荷載矢量、等效剛度,至此,第0段的反應已經計算完畢,已經有了初始量,可以進入疊代計算。
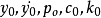
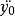
第i+1段(i=1,2,3...)
先利用第i段的量做好準備工作:等效剛度、荷載矢量、等效剛度。
然後開始求第i+1段的量。
