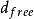簡介
糾錯碼(error correcting code) ,是在接收端能自動地糾正數據傳輸中所發生差錯的碼。糾錯碼的基本思路是在所有的由傳送符號組成的序列中,僅挑出其中一部分做為信息的代表向信道傳送,並使得所挑出的這些序列之間有儘可能多的差異。每個被挑出的允許傳送的序列被稱為一個碼字,而碼字的總合稱為碼。在傳送端把信息變換成碼字的過程稱為編碼;在接收端從接收到的信號判定所發碼字、從而恢覆信息的過程稱為解碼(或解碼)。在解碼時,若收到的信號不是碼中的一個碼字,則可以肯定在傳輸中出現了差錯,從而著手對差錯進行糾正。糾錯的方法是找到與接收到的信號最接近的碼字,並將其判定為傳送信號。一般採用“距離”來度量信號間的接近程度,一種常用的“距離”稱為漢明距離,它被定義為兩碼字間對應位不同的個數總和。一個給定碼,其全部碼字兩兩之間距離的最小值被稱為這個碼的碼距。碼距是一個碼糾錯能力的重要參數,例如在漢明距離下,若接收到的信號出錯的位數不多於碼距的一半,則接收端總能正確地恢復所傳送的碼字,從而正確地恢復所傳送的信息。
糾錯編碼又稱
信道編碼,它與信源編碼是信息傳輸的兩個方面。它們之間存在對偶的關係。套用
信道解碼直接對一些自然信息進行處理,可以去掉
剩餘度,以達到壓縮數據的目的。
為了使一種碼具有檢錯或糾錯能力,必須對原碼字增加多餘的
碼元,以擴大碼字之間的差別,使一個碼字在一定數目內的碼元上發生錯誤時,不致錯成另一個碼字。準確地說,即把原碼字按某種規則變成有一定
剩餘度的碼字,並使每個碼字的
碼元間有一定的關係。關係的建立稱為編碼。碼字到達收端後,用編碼時所用的規則去檢驗。如果沒有錯誤,則原規則一定滿足,否則就不滿足。由此可以根據編碼規則是否滿足以判定有無錯誤。當不能滿足時,在可糾能力之內按一定的規則確定錯誤所在的位置,並予以糾正。糾錯並恢復原碼字的過程稱為
解碼;
碼元間的關係為線性時,稱為線性碼;否則稱為
非線性碼。檢錯碼與其他手段結合使用,可以糾錯。檢錯反饋重發系統(ARQ系統)就是一例。
在構造糾錯碼時,將輸入信息分成
k位一組以進行編碼。若編出的校驗位僅與本組的信息位有關,則稱這樣的碼為
分組碼。若不僅與本組的
k個信息位有關,而且與前若干組的信息位有關,則稱為格碼。這種碼之所以稱為格碼,是因為用圖形分析時它象籬笆或格架。線性格碼在運算時為卷積運算,所以叫
卷積碼。
發展過程
C.E.仙農在1948年發表在《通信的數學理論》一文中的
信道編碼定理指出:只要採用適當的糾錯碼,就可在多類信道上傳輸訊息,其
誤碼率pe可以任意小 (1)式中
n為碼長;
Er(
R)為信息率
R的函式,與
信道有關。當
R小於
信道容量C時,
Er(
R)為正值。可惜的是這一定理僅僅指出理論上可以達到的目標,而未能給出構造性的實現方法。自仙農的論文發表以來,人們經過持續不懈的努力已找到多種好碼,可以滿足許多實用要求。但在理論上,仍存在一些問題未能解決。
漢明碼
R.W.漢明於1950年首先給出可以糾正一個獨立錯誤的線性
分組碼──漢明碼。差不多與此同時E.戈雷給出一種可以糾正三個錯誤的完備碼。完備碼雖然十分罕見,但有較大實用意義。1954年D.E.莫勒提出一種能糾正多個錯誤的碼;I.S.里德則立即給出它的
解碼方法,用的是擇多判決法,這種碼常稱為RM碼。1957年,E.普勒齊引入了循環碼的概念。1959~1960年出現了BCH碼,引進有限域的概念,解決了循環碼的構造和性能估計等基本問題。後來成為線性
分組碼中最重要的一類碼。它能糾正多個錯誤,且在實用範圍內接近
信道編碼定理所指出的
誤碼率值。但當
n增大時,其
誤碼率不能呈指數下降。BCH碼的
解碼問題是W.W.彼得森解決的;錢天聞則提供了一種系統地搜尋根的方法。1967年,E.R.伯利坎普提出一種
疊代算法,大大簡化了
解碼,使糾錯碼趨於實用。1970年В.Д.戈帕提出一種線性
分組碼的
構造方法,原則上它可以達到吉爾伯特限,實現了理論上預期的目標。但至今仍未解決如何具體構造這種碼的問題。
卷積碼最早由P.伊萊亞斯於1955年提出。它的糾錯能力較強,設備複雜程度與
分組碼大體相當。首先獲得成功的
解碼方法是序列解碼。1967年A.J.維特比提出的
解碼算法,能較好地按最大似然準則解碼,且在許多領域中均可套用。
卷積碼還可用代數方法
解碼。它的設備雖較簡單,但性能較差。
卷積碼在理論上不如
分組碼成熟,所用的工具也比較多樣,尚缺乏系統的、統一的方法處理。
為了實現低的
誤碼率,根據式(1),要求碼長
n較大。但已知的大多數碼,當
n變大時不是性能欠佳或者難以構造,就是
解碼過分複雜,不容易實現。但是,可以利用好的碼進行級連,以得到性能更好的碼。級連碼的
內碼和外碼,用
分組碼和
卷積碼都可以。這在深空通信中套用較多。
基本原理和性能參數
糾錯碼能夠檢錯或糾錯,主要是靠碼字之間有較大的差別。這可用碼字之間的漢明距離
d(
x,
y)來衡量。它的定義為碼字
x與
y之間的對應位取不同值的
碼元個數。一種糾錯碼的最小距離
d定義為該種碼中任兩個碼字之間的距離的最小值。一種碼要能發現
e個錯誤,它的最小距離
d應不小於
e+1。若要能糾正
t個錯誤,則
d應不小於2
t+1。一個碼字中非零
碼元的個數,稱為此碼字的
漢明重量。一種碼中非零碼字的重量的最小值,稱為該碼的最小重量。對線性碼來說,一種碼的最小重量與其最小距離在數值上是相等的。
在構造線性碼時,數字上是從
n維空間中選一
k維子空間,且使此子空間內各非零碼字的重量儘可能大。當構造循環碼時,可進一步將每一碼字看成一多項式,將整個碼看成是多項式環中的理想,這一理想是主理想,故可由生成多項式決定;而多項式完全可由它的根規定。這樣,就容易對碼進行構造和分析。這是BCH碼等循環碼構造的出發點。一般地說,構造一種碼時,均設法將它與某種代數結構相聯繫,以便對它進行描述,進而推導它的性質,估計它的性能和給出它的解碼方法。若一種碼的碼長為
n,碼字數為
M,或信息位為
h,以及最小距離為
d,則可把此碼記作【
n,
M,
d】碼。若此碼為線性碼,常簡記作(
n,
k)或(
n,
k,
d)碼。人們還常用
R=log2
M/
n表示碼的信息率或簡稱
碼率,單位為比特/
碼元。
R越大,則每個
碼元所攜帶的信息量越大,編碼效率越高。
實現
糾錯碼實現中最複雜的部分是
解碼。它是糾錯碼能否套用的關鍵。根據式(1),採用的碼長
n越大,則誤碼率越小。但
n越大,編解碼設備也越複雜,且延遲也越大。人們希望找到的
解碼方法是:誤碼率隨碼長
n的增加按指數規律下降;解碼的複雜程度隨碼長
n的增加接近線性地增加;解碼的計算量則與碼長
n基本無關。可惜,已經找到的碼能滿足這樣要求的很少。不過由於大規模積體電路的發展,即使套用比較複雜的但性能良好的碼,成本也並不太高。因此,糾錯碼的套用越來越廣泛。
糾錯碼傳輸的都是數位訊號。這既可用硬體實現,也可用
軟體實現。前者主要用各種數字電路,主要是採用大規模積體電路。
軟體實現特別適合計算機通信網等場合。因為這時可以直接利用網中的計算機進行編碼和
解碼,不需要另加專用設備。硬體實現的速度較高,比
軟體可快幾個數量級。
在傳信率一定的情況下,如果採用糾錯碼提高可靠性,要求
信道的傳輸率增加,頻寬加大。因此,糾錯碼主要用於功率受限制而頻寬較大的
信道,如衛星、散射等系統中。糾錯碼還用在一些可靠性要求較高,但設備或器件的可靠性較差,而餘量較大的場合,如磁帶、磁碟和
半導體存儲器等。
在
分組碼的研究中,譜分析的方法受到人們的重視。糾
同步錯誤碼、算術碼、不對稱碼、不等錯誤糾正碼等,也得到較多的研究。
分組碼
分組碼是對信源待發的信息序列進行分組(每組K位)編碼,它的校驗位僅同本組的信息位有關。自20世紀50年代
分組碼的理論獲得發展以來,分組碼在數字通信和數據存儲系統中已被廣泛套用。
分組碼的碼長n和碼字個數M是一個碼的主要構造參數。碼長為n的碼中所有碼字的位數均為n;若要用一個碼傳送k比特信息,則碼字的個數M必須滿足
。典型的分組碼是由k位信息位和r位監督位組成的,這樣構成的碼一般稱為系統碼。
分組碼中套用最廣的線性分組碼。線性分組碼中的M個碼字之間具有一定線性約束關係,即這些碼字總體構成了n維線性空間的一個k維子空間。稱此k維子空間為(n,k)線性分組碼。線性系統碼的特點是每個碼字的前k位均由這個碼字所對應的信息位組成,並通過對這k位信息位的線性運算得到後面n—k是位監督位。
線性分組碼中套用最廣的是循環碼,循環碼的主要特徵是任何碼字在循環移位後個碼字。循環碼的優點在於其編碼和解碼手續比一般線性碼簡單,因而易於在設備上實現。在循環碼中,碼字
可表示為多項式
。循環碼的碼字多項式都可表示成為循環碼的生成多項式
與這個碼字所代表的信息多項式
的乘積,即
,因此一個循環碼可以通過給出其生成多項式
來規定。常用的循環碼有BCH碼和RS碼。
 圖1 碼率為1/2、四種狀態的格線碼的格線圖
圖1 碼率為1/2、四種狀態的格線碼的格線圖格線碼有多種描述方法,格線圖是常用方法之一,它能表示出編碼過程。一個碼率為1/2、包含四種狀態的格線碼的格線圖如圖所示。圖1中00,01,10,11表示編碼器所具有的四種狀態,以“·”示出,從每一狀態出發都存在兩條支路,位於上面的一條支路對應於編碼器輸入為“0”的情況,位於下面的一條支路對應於編碼器輸入為“1”的情況,而每一支路上所列出的兩個二進位碼則表示相應的編碼輸出。因而可知,編碼輸出不僅決定於編碼器的當前輸入,還決定於編碼器的狀態,例如在圖中從“00”狀態出發;,若輸入的二進制數據序列為1011,則編碼器的狀態轉移過程為00→01→10→01→11,而相應的編碼輸出序列為11010010。在格線圖中任意兩條從同一狀態出發;,經不同的狀態轉移過程後又歸於另一相同狀態(該狀態也可與初始狀態相同)的路徑間的距離的最小值稱為碼的自由距離
。如該圖中的
為5。對於卷積碼來說,
的計算可簡化為始於且終於零狀態的非全零路徑與全零路徑間距離的最小值。
是表征格線碼糾錯能力的重要參數。維特比算法是廣泛採用的格線碼的解碼方法。由於格線碼的狀態越多,解碼越複雜,所以狀態個數是度量格線碼解碼複雜性的重要參數。一般說來可以通過增大解碼複雜性來增加
,從而提高碼的糾錯能力。
BCH碼、格線碼已被廣泛地套用於移動通信、衛星通信和頻帶數據傳輸中。RS碼也被廣泛套用於光碟的存儲中。
大多數糾錯碼是設計來糾隨機誤碼的,可以通過交織的方法使它適用於對突發誤碼的糾錯。交織是一種使得集中出現的突發誤碼在解碼時進行分散化的措施,從而使其不超出糾錯碼的糾錯能力範圍。
卷積碼
卷積碼不對信息序列進行分組編碼,它的校驗元不僅與當前的信息元有關,而且同以前有限時間段上的信息元有關。
卷積碼在編碼方法上尚未找到像
分組碼那樣有效的數學工具和系統的理論。但在
解碼方面,不論在理論上還是實用上都超過了
分組碼,因而在
差錯控制和
數據壓縮系統中得到廣泛套用。







 圖1 碼率為1/2、四種狀態的格線碼的格線圖
圖1 碼率為1/2、四種狀態的格線碼的格線圖

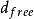









 圖1 碼率為1/2、四種狀態的格線碼的格線圖
圖1 碼率為1/2、四種狀態的格線碼的格線圖