節點阻抗矩陣,是把多連線埠網路中電流,電壓以及阻抗的關係以矩陣的方式所呈現。阻抗矩陣又稱開路阻抗矩陣。與阻抗矩陣對應的是導納矩陣,二者的區別在,阻抗矩陣是以端電流為激勵,而導納矩陣是以端電壓為激勵,不過二者描述的問題實質是一個,只不過是兩種表述方式。
基本介紹
- 中文名:節點阻抗矩陣
- 外文名:Impedance matrix
- 套用領域:多連線埠網路
- 別名:開路阻抗矩陣
- 對應概念:導納矩陣
- 實質:反映電壓和電流關係
定義
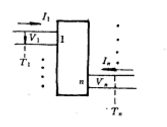
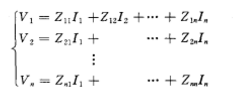
相關導納矩陣
矩陣特性
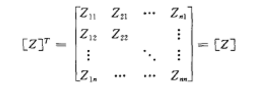
相關推論
歸一化方法
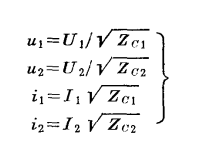
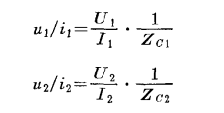
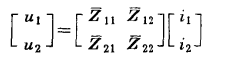
節點阻抗矩陣,是把多連線埠網路中電流,電壓以及阻抗的關係以矩陣的方式所呈現。阻抗矩陣又稱開路阻抗矩陣。與阻抗矩陣對應的是導納矩陣,二者的區別在,阻抗矩陣是以端電流為激勵,而導納矩陣是以端電壓為激勵,不過二者描述的問題實質是一個,只不過是兩種表述方式。

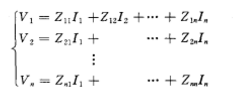
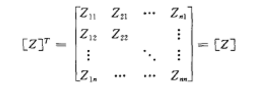
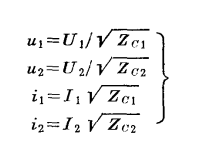
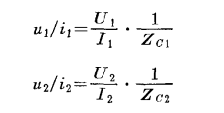
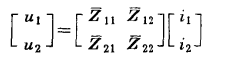
節點阻抗矩陣,是把多連線埠網路中電流,電壓以及阻抗的關係以矩陣的方式所呈現。阻抗矩陣又稱開路阻抗矩陣。與阻抗矩陣對應的是導納矩陣,二者的區別在,阻抗矩陣是以端...
節點阻抗矩陣 目錄 1 簡介 2 二連線埠網路 3 N連線埠網路 節點導納矩陣簡介 編輯 在進行微波系統分析時,可以把一個微波系統用一個電路和網路來等效,從而把一個本...
因此根據式(1)可得以節點阻抗矩陣為網路參數的節點電壓方程。節點阻抗矩陣的對角元素Zii稱自阻抗,非對角元素Zij(i≠j)稱為節點i、j之間的互阻抗。節點阻抗矩陣...
第2章電力系統網路矩陣2.1節點導納矩陣2.1.1節點導納矩陣的性質及物理意義2.1.2節點導納矩陣的建立2.1.3節點導納矩陣的修改2.2節點阻抗矩陣...
8-4 套用節點阻抗矩陣計算不對稱故障8-5 複雜故障的計算方法小結習題附錄Ⅰ 電感的計算附錄Ⅱ 線性方程組的直接解法附錄Ⅲ 常用的網路等值變換...
而每個電網的短路計算都牽涉到鄰接電網的阻抗陣,為了減少數據通信量,這就需要每個電網的EMS/SCADA 能快速地把本網的節點阻抗矩陣化簡為邊界節點等值阻抗矩陣並傳送給...
第二節 節點阻抗矩陣第三節 電力網路方程的求解方法第四節 節點編號順序的最佳化習題第二章 電力系統潮流計算第一節 概述第二節 潮流計算的數學模型...
第二節 電力系統故障計算用的等值網路及其節點方程第三節 系統故障時網路電氣量的計算第四節 節點導納矩陣(y)的形成第五節 求節點阻抗矩陣的方法...
15.3 節點阻抗矩陣及其算法小結思考題與習題第16章 電力系統故障的計算機算法16.1 概述16.2 對稱故障的計算機算法16.3 簡單不對稱故障的計算機算法...
7.4.2用節點阻抗矩陣的計算方法7.4.3用節點導納矩陣的計算方法7.4.4短路點線上路上任意處的計算小結思考題習題第8章電力系統不對稱故障的分析與計算...
由支路阻抗形成對稱網路的節點阻抗矩陣,抽取邊界節點所對應的元素即可組成式Zbn.012。如果正常狀況的系統是對稱的,也可先形成全系統的節點阻抗矩陣,再切除故障後不...
1.2.2 節點阻抗矩陣的特點及其元素的物理意義1.2.3 節點阻抗矩陣元素的求解方法1.2.4 節點阻抗矩陣元素的實數化求解方法思考題...
第四節 節點阻抗矩陣第三章 電力系統潮流計算第一節 節點功率方程第二節 牛頓-拉夫遜法第三節 P-Q分解法第四章 電力系統短路電流計算...
4-3 節點阻抗矩陣 4-4 節點編號順序的最佳化 小結 習題 第五章 電力系統三相短路的暫態過程 5-1 短路的一般概念 5-2 恆定電勢源電路的三相短路 5-3 同步電機...
電力系統網路矩陣,電力網路計算中的稀疏技術,網路方程的修正解法,網路變換、化簡...第2章 電力系統網路矩陣2.1 節點導納矩陣2.2 節點阻抗矩陣2.3 節點導納矩陣...
基於節點阻抗矩陣的配電網故障測距算法[J]. 電網技術,2013,11:3233-3240. (EI收錄) 鄭濤,陳佩璐,劉連光,毛安瀾. 地磁感應電流對電流互感器傳變特性及差動...
6-2 電力系統故障計算用的等值網路及其節點方程6-3 電力系統故障時網路電氣量的計算6-4 節點導納矩陣(Y)的形成6-5 求節點阻抗矩陣(z)的方法6-6 導納型節點...
外部網路的諾頓等值模型參數包括連線埠的等值注入功率、節點阻抗矩陣和外邊界節點的電壓,如圖1(b)中的Sm、Sn、zm0、zi0、zmn、Vm和Vn。通過高斯消去法對外部網路...
利用支路斷開前的節點阻抗矩陣數據,估算雙重支路開斷後的電流分布係數,原理與前述算法類似。廣域繼電保護系統研究的難點和建議 從仿真結果看,以上潮流轉移識別算法的...
[2]孫銀鋒,吳學光,湯廣福,李國慶,“基於節點阻抗矩陣GS法的直流電網穩態潮流計算”,中國電機工程學報,35(8),2015: 1882-1892. [3]李國慶,孫銀鋒,吳學光,“柔...
