多區系統

多區系統是指由多區域控制器匯合連線形成的綜合管理區域網。例如在多區域空調系統中，由於多區效應的存在，使得在滿足各區域空氣品質要求與降低能耗之間的權衡成了一個很大的難題。

基本介紹

• 中文名：多區系統
• 外文名：multi-site system
• 描述：多區域綜合管理區域網
• 套用：多區域空調系統
• 學科：信息技術

概念

多區系統（multi-site system）由多個單區網通過區域控制器連線而成的分級管理區域網。這樣在一個地域中可以有多個不一定相鄰接的區，各區設單區網。每個單區網的控制中心通過無線或有線方式與區域控制器相連，並且受其控制和管理。

多區系統的新風控制策略的研究

研究背景

根據ASHRAE Standard62—2001中的要求，空調系統的送風一方面要有效地消除室內多餘的熱負荷，另一方面要保證室內的空氣品質達到“可接受”的程度，為此制定了各類用途建築物的最小新風量。但在實際的多區域送風系統中，從總體上達到最小新風量只符合系統級控制的要求，而從區域級控制上考察，則完全不可接受。

空調區域的負荷由照明熱、人體熱、設備熱以及太陽輻射熱等組成，可以通過調節每個區域的VAV風箱改變送風量，以滿足區域的冷負荷要求。區域的新風需求根據用途及其使用者的活動狀況確定，因此它的值在不同區域、甚至同一區域的不同時刻都完全不同，這就造成各個區域需求新風比的不同。通常情況下，由一個AHU服務的多區域，它們的新風比是相同的。因此對於AHU新風比高於需求新風比的區域，送入的新風量超過了需求量，區域的空氣品質雖然大大提高，但也浪費了能量；而AHU新風比小於需求新風比的區域，由於新風不足，區域中污染物不能有效地稀釋，會導致空氣品質惡化，影響室內人員的身體健康。要避免個別區域的通風不足，有4種方法：

(1)增大AHU新風比y，滿足各個區域的新風需求；

(2)提高送風溫度，增大送風量，在AHU新風比不變的情況下提高流入區域的新風量；

(3)採用ASHRAE標準的多區方程對新風比進行修正，充分利用迴風中尚未被利用的新風；

(4)保持AHU新風比不變，用末端再熱的方法增加通風不足區域的熱負荷，以提高其送風量，從而加大新風供給。

由於第4種方法的關鍵是回熱，而它在動態工況的控制中存在一個嚴重問題:再熱器的熱延遲。由於再熱器的熱容、功耗和放熱量之間有一定的時間延遲，這個延遲將導致再熱效果變差，能耗增大。在這方面的研究主要集中在預測數學的引入，但效果並不很理想。

新風控制方案

（1）最大新風比策略(MaxY策略)

AHU新風比根據臨界區域(新風比要求最大的區域)的新風比確定，這樣可以滿足各個區域的新風要求，但是新風負荷必然相當大，除了臨界區域外，其它區域都處於過量通風的狀態。因此MaxY策略是一種以較高的耗能來換取空氣品質的策略。

（2）提高送風溫度策略(SAT—Reset策略)

在部分負荷情況下，提高AHU的送風溫度，可以增加各個區域的送風量，在系統新風比不變的情況下，各區域中送入的新風量就會增大，從而滿足臨界區域的新風需求。這種方法的優點在於因為採用了較大的送風量，可以使室內的空氣與新風混合得更加均勻，達到更好的稀釋效果。但增大風量的同時風機能耗也上升，而且送風溫度提高，使得系統對空調區域的濕度控制能力相應減弱。

研究結論

最大新風(MaxY)策略採用了臨界區域的新風比作為系統新風比，因此有大量區域處於過量通風狀態，通過測量室內CO₂濃度，可見看到這種策略可以得到最好的空氣品質，而能耗方面和SAT—Reset策略相差不大，甚至略低，但要高於MSE策略。

提高送風溫度(SAT—Reset)策略的送風量最大，這有助於區域內空氣的均勻混合，因而可以得到較好的舒適性，但勢必增加送、迴風機的能耗，因此提高送風溫度在能耗方面可能有所增加，同時送風溫度提高了，對區域的濕度控制作用必然有所削弱。

基於諾頓等值的多區系統最佳化分解協調算法

傳統的無功最佳化計算方法在計算速度上還不能滿足大規模電力系統實時控制的要求。將分布在不同區域的計算機通過網路互聯，採用高性能的計算機技術和最佳化算法對大型互聯繫統實施分析和計算已經成為可能。如何高效地運用現有計算資源通過並行計算實現大規模電力系統無功最佳化分散式線上計算，具有重要意義。

潮流和最優潮流並行計算的基本思想是：按實際地理位置或物理結構，將電力系統分解為多個區域，區域間採用某種方式進行協調修正。主要方法有：節點分裂法，相當於在區域之間的聯絡線上插入電壓源，用其電壓作為計算中的協調變數；支路切割法，相當於在區域間的聯絡線上插入電流源以代替各子區域間狀態變數的影響，用其電流作為計算的協調變數；利用矩陣理論的處理方法，如對角加邊模型、重疊分塊牛頓法、加速重疊分塊牛頓法等；外部網路等值法，主要採用Ward等值和戴維南等值。

研究將採用節點分裂法將電力系統按照實際地理位置進行區域分解，通過對外部系統進行諾頓等值，實現各個區域無功最佳化的獨立計算，即內層疊代計算，並引入一套簡單有效的協調機制修正邊界節點的等值注入功率和電壓，即外層疊代計算，最終實現大系統無功最佳化分解與協調計算，提高計算效率。該算法強調各區域地位平等，不分主次，各自數據資源相互獨立，以各區域電網之間的少量數據交換來實現無功最佳化協調分散式計算，並且保證各區域在最佳化過程中均可監視與其它區域之間的聯絡線潮流功率變化。

系統分區及諾頓等值

以圖1兩區域系統為例，說明內部節點、邊界節點及外部系統的諾頓等值電路概念。圖1(a)為原系統接線圖，該系統由區域A1和A2構成，它們通過聯絡線Lim和Ljn相連。聯絡線的端點i、j、m和n統稱為邊界節點，用集合B表示。對於區域A1而言，定義節點m和n為外邊界節點，用集合B_E表示，其節點電壓幅值和相角表示為x_BE；定義節點i和j為內邊界節點，用集合B_I表示，其節點電壓幅值和相角表示為_xBI。同理，對於區域A2而言，定義節點i和j為外邊界節點，節點m和n為內邊界節點。用I代表區域A1或A2的內部節點集，節點電壓幅值、相角，發電機和無功補償裝置的無功出力等變數表示為x₁。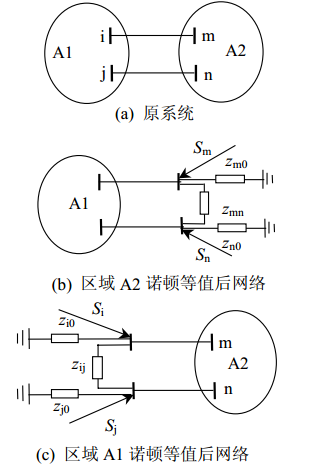

圖1 兩區域系統分解及其諾頓等值

在對區域A1進行最佳化計算時，以其外邊界節點m、n及地節點構成多連線埠，根據諾頓等值原理對區域A2進行外部等值，如圖1(b)所示。z_m0、z_n0和z_mn表示外部網路的諾頓等值阻抗，S_m和S_n表示外部網路的等值注入功率。類似地，在對區域A2進行最佳化計算時，也可根據諾頓等值原理對區域A1進行外部等值，如圖1(c)所示。z_i0、z_j0和z_ij表示外部網路的諾頓等值阻抗，S_i和S_j表示外部網路的等值注入功率。值得注意的是，以外邊界節點和地節點組成的多連線埠對外部網路實施諾頓等值，可以保證各區域在最佳化過程中均可監視與其它區域之間的聯絡線潮流功率變化。

無功最佳化分解協調算法

（1）諾頓等值參數的求取

外部網路的諾頓等值模型參數包括連線埠的等值注入功率、節點阻抗矩陣和外邊界節點的電壓，如圖1(b)中的S_m、S_n、z_m0、z_i0、z_mn、V_m和V_n。通過高斯消去法對外部網路進行變換得等值模型導納矩陣，對其求逆，即可得到連線埠節點阻抗矩陣。等值注入功率和外邊界節點的電壓可由2條途徑獲得：一是每次通過網路變換得到精確的外部網路等值模型，此方法固然可以逐步提高等值精度，最終獲得與集中最佳化相同的結果，但實現存在諸多困難，如：等值注入功率的計算量較大；二是以基態時聯絡線潮流值作為等值注入功率初值，基態時的外邊界節點電壓值作為其電壓初值。當內層疊代結束後，在各區域內部節點變數確定的前提下，等值注入功率和外邊界節點電壓可以通過外層疊代進行修正，逐步提高外部網路等值模型的精度。與內層疊代的交替使用，最終可獲得精確的等值參數。顯然第2種方法的計算量比第1種小。在無功最佳化過程中，外邊界節點電壓和等值注入功率易於得到。

（2）各區域功率平衡原則

在集中最佳化計算中，通常取一個平衡節點，既作為整個電網有功功率平衡點也作為全網節點電壓相角的參考點。為與集中最佳化結果保持一致，在分散式計算中，原平衡節點仍作為其所在區域的平衡節點，對於不含原平衡節點的其它區域，在計算過程中功率無法平衡時，其缺額從外邊界節點注入。通常無功本著就地平衡的原則，較易實現平衡，邊界注入功率對有功平衡影響較大。

（3）參考節點選取及電壓相角修正

為實現各個區域無功最佳化的獨立計算，不同區域應該取不同的參考節點。原平衡節點仍作為其所在區域的參考節點，對於不含原平衡節點的其它區域，取其某一個外邊界節點為參考節點。在各區域的最佳化計算完成後，再對其它區域的節點電壓相角進行修正，折算到統一的參考節點(原平衡節點)上。

計算步驟

無功最佳化分解協調計算步驟如下：

1）預備階段，對全網進行初始潮流計算和分區，計算各區域的外部網路等值阻抗。

2）內層疊代計算，求取各區域外部網路諾頓等值模型參數，並套用非線性原對偶內點法，分別獨立進行無功最佳化計算。其收斂判據為補償間隙g<10^-5，最大潮流偏差e<10^-3。

3）用式(1)(2)修正各區域(不含平衡節點)節點電壓相角。

4）檢驗邊界節點電壓是否滿足收斂條件。如果滿足，則整個計算結束；否則，轉第5）步。其收斂判據為相同邊界節點電壓在不同區域中最佳化計算結果滿足：電壓幅值之差的絕對值小於10^-3，電壓相角之差的絕對值小於0.01。

5）外層疊代計算，修正各個區域外部網路的諾頓等值模型參數。

6）計算各區域功率缺額，並採用調整邊界節點注入有功功率的方法實施平衡，然後轉第2）步。

算法誤差分析

對不含原平衡節點的區域，將功率缺額人為分配給外邊界節點的等值注入，給計算結果帶來一定誤差。從無功最佳化的角度考慮：算例各子區域有功缺額不大，因此分配邊界節點有功等值注入所帶來的計算誤差相對較小。無功最佳化計算過程中，無功潮流分布變動相對較大，因此邊界節點的無功等值注入所產生的誤差相對較大，但無功潮流分布變化所產生的誤差取決於邊界節點的無功支撐路徑。如果某邊界節點的無功支撐來自相同區域，則通過邊界節點的注入量相對較小，所產生計算誤差較小。如果邊界節點的無功支撐來自其它區域，則通過人為分配等值注入無功功率造成的計算誤差相對較大。從表1可以看出，研究的分解協調算法在套用中均能較快收斂到最優點，表明算例各子區域均能實現無功功率的自我滿足。對產生較大誤差的算例，某些子區域無功功率難以實現自我滿足，需要從其它區域注入。通過對系統區域分解，從無功支撐路逕入手進行分區(如：用基於無功電壓靈敏度的分區方法等)，可實現各個子區域無功功率的自我滿足，減小了計算誤差。

表1 分解協調算法得到的結果

研究結論

1）對於區域間具有強耦合或弱耦合的大系統均可使用，且各子區域地位平等。

2）在最佳化過程中，容易獲取採用多連線埠注入功率和阻抗表示的諾頓等值模型參數，並能實現跟蹤修正，達到了較好的分解協調效果。用各區域間較小的數據交換量取得了較好的計算效果，並能對區域間的聯絡線潮流功率變化進行監控。