算術差(arithmetical difference)是指一種數論函式,也叫做點減。設兩個自然數x,y,則x與y的算術差在x≥y時,其值為x-y;其他情況,其值為0。與通常的差函式相應的另一個數論函式是絕對差,其值為x、y之差的絕對值|x-y|。
基本介紹
- 中文名:算術差
- 外文名:arithmetical difference
- 別名:點減
- 性質:一種數論函式
- 相應函式:絕對差
- 學科:數學
簡介







數論函式



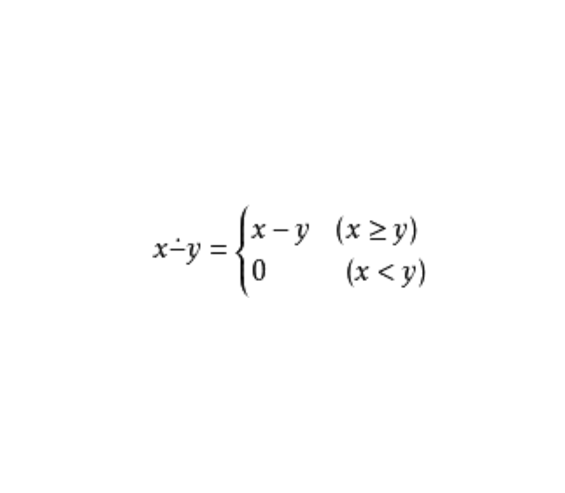
算術差(arithmetical difference)是指一種數論函式,也叫做點減。設兩個自然數x,y,則x與y的算術差在x≥y時,其值為x-y;其他情況,其值為0。與通常的差函式相應的另一個數論函式是絕對差,其值為x、y之差的絕對值|x-y|。










算術差(arithmetical difference)是指一種數論函式,也叫做點減。設兩個自然數x,y,則x與y的算術差在x≥y時,其值為x-y;其他情況,其值為0。與通常的差函式相應的另一個數論函式是絕對差,其值為x...
在古代全部數學就叫做算術,現代的代數學、數論等最初就是由算術發展起來的。後來,算學、數學的概念出現了,它代替了算術的含義,包括了全部數學,算術就變成了其中的一個分支。基本介紹 算術(arithmetic)是數學的一個基礎分支。它以...
的算術平方根;零的平方根也叫做零的算術平方根,因此零的算術平方根仍舊為零。各部分的關係 乘法是加法的簡便運算,除法是減法的簡便運算。減法與加法互為逆運算,除法與乘法互為逆運算。加數+加數=和;被減數-減數=差;一個加數=和...
第二篇討論一次同餘方程:其中嚴格證明了算術基本定理。第三篇討論冪的同餘式:此篇詳細討論了高次同餘式。第四篇“二次同餘方程”意義非同尋常:因為其中給出了二次互反律的證明,有人統計到21世紀初,二次互反律的證明已經超過200...
算術運算符即算術運算符號。是完成基本的算術運算 (arithmetic operators) 符號,就是用來處理四則運算的符號。套用 算術運算 (arithmetic operators) 符號,就是用來處理四則運算的符號,這是最簡單,也最常用的符號,尤其是數字的處理,...
數字電路能完成的算術功能有加法、減法、乘法和除法等。這與模擬電路中的比例運算、求和運算以及模擬乘法器等是不一樣的概念。模擬電路的運算完成的是對信號幅值的一種疊加.而數字電路的算術功能完成的是純數字的運算,這些數字必須以二...
算術平均溫差 算術平均溫差(arithmetic mean temperature difference)是1995年公布的化學工程名詞。公布時間 1995年,經全國科學技術名詞審定委員會審定發布。出處 《化學工程名詞》第一版。
算術和也稱為區間分析,是定義在區間上的一組運算規則。其主要特點是能處理不確定數據,自動記錄計算機浮點運算中所產生的截尾和捨入誤差,高效而可靠地估計函式在某個自變數區域的取值範圍,從而被廣泛套用於自然科學的各個領域。算術和定義...
重差術是一種測量方法。內容簡介 《九章算術》中《勾股》章的最後幾個問題,乃是測量城池、山高和井深之的測量問題,這種測量方法稱為「重差術」。 三國時代數學家劉徽為了解釋「重差術」,便撰寫《重差》一卷,附在《九章算術》...
1889年,在數學家戴德金工作的基礎上,皮亞諾在《用一種新方法陳述的算術原理》一書中提出了一個算術公理系統,這個公理系統有九條公理,其中四條是關於“相等”的,五條是刻畫數的,並且以1而不是0作為基本概念。在後來的著作中,...
剩餘誤差(residual errors)是各次測量值與其算術平均值之差,也稱殘差、殘餘誤差。在等精度測量中,x為算術平均值;在不等精度測量中,x為加權平均值。 可以證明殘差的代數和等於零和殘差的平方和為最小值。 這兩點特性是檢驗算術平均...
《勾股六術》清項名達撰。勾股六術(Gougu liushu )《下學庵算術三種》中的一種一卷,清項名達撰,成書於1825年,是一本講述勾股算術的人門書.勾股形的勾股弦及其和差共有13種,已知任何其中2種,皆可求解勾股形,計有78題.該...
更相減損術是出自《九章算術》的一種求最大公約數的算法,它原本是為約分而設計的,但它適用於任何需要求最大公約數的場合。思想 《九章算術》是中國古代的數學專著,其中的“更相減損術”可以用來求兩個數的最大公約數,原文是:白...
平均差(Mean Deviation)是表示各個變數值之間差異程度的數值之一。指各個變數值同平均數的離差絕對值的算術平均數。平均差異大,表明各標誌值與算術平均數的差異程度越大,該算術平均數的代表性就越小;平均差越小,表明各標誌值與算術...
同義詞 SD(標準差)一般指標準偏差 標準偏差(Std Dev,Standard Deviation) -統計學名詞。一種度量數據分布的分散程度之標準,用以衡量數據值偏離算術平均值的程度。標準偏差越小,這些值偏離平均值就越少,反之亦然。標準偏差的大小可通過...
。也就是說,標準差的平方即為方差。方差也是最廣泛使用的離散程度測量值。根據研究對象範圍差異方差可分為總方差、組內方差和組間方差。總方差是由總體變數值和總體算術平均數計算出來的方差。見式(1)和式(2)。反映總體內所有變數值...
以下數值均取6位有效數字,為使排版整齊,此處一律省略√ ̄(算術平方根則取其正值)計算公式 成立條件:a≥0,n≠0。成立條件:a≥0, n≠0。成立條件:a≥0,b≥0,n≠0。成立條件:a≥0,b>0,n≠0。成立條件:a≥0,n...
誤差可以用絕對誤差和相對誤差來表示。絕對誤差是分析結果與真值之差,表示為:Eₐ=x-T x代表單次測定值。由於測定次數往往不止一次,因此通常用數次平行測定結果的算術平均值來表示分析結果。此時:Eₐ=x-T 相對誤差是絕對誤差和...
平方根,又叫二次方根,表示為〔±√ ̄〕,其中屬於非負數的平方根稱之為算術平方根(arithmetic square root),是一種方根。一個正數有兩個實平方根,它們互為相反數,負數在實數範圍內沒有平方根,0的平方根是0。定義 如果一個...
2.2 算術平均值原理 2.2.1 算術平均值 2.2.2 測量標準差與極限誤差 2.3 加權算術平均值原理 2.3.1 測量數據的權 2.3.2 加權算術平均值 2.3.3 加權算術平均值的標準差與極限誤差 2.4 異常數據的發現與處理 2.4.1 ...
