剩餘誤差

剩餘誤差（residual errors）是各次測量值與其算術平均值之差，也稱殘差、殘餘誤差。在等精度測量中，x為算術平均值；在不等精度測量中，x為加權平均值。 可以證明殘差的代數和等於零和殘差的平方和為最小值。 這兩點特性是檢驗算術平均值是否正確的依據，也是建立最小二乘法的理論依據。殘差在誤差理論中是一個經常遇到的重要參數。

基本介紹

• 中文名：剩餘誤差
• 外文名：residual errors
• 別稱：殘差、殘餘誤差
• 套用學科：數學（誤差理論）
• 相關概念：算術平均值等

隨機誤差的特徵

一般就隨機誤差的個體而言，其大小和方向都無法預測，而就隨機誤差的總體而言，則具有統計規律性，服從某種機率分布。大量實驗證明，隨機誤差服從以下統計特徵：

(1)絕對值相等的正誤差與負誤差出現的次數相等，稱為隨機誤差的對稱性；

(2)絕對值小的誤差比絕對值大的誤差出現的次數多，稱為隨機誤差的單峰性；

(3)在一定的測量條件下，隨機誤差的絕對值不會超過一定界限，稱為隨機誤差的有界性；

(4)當測量次數增加，隨機誤差的代數和趨向於零，稱為隨機誤差的抵償性。

隨機誤差的機率分布

隨機誤差的機率分布有常態分配、均勻分布、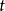分布、反正弦分布、梯形分布、三角分布等。絕大多數隨機誤差服從常態分配，因此，常態分配規律占有重要地位。

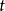
常態分配的隨機誤差，其機率密度函式為

式中 和——隨機誤差的方差和標準差，標準差定義為方差的正的算術平方根；

被測量的真值；

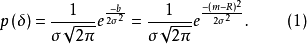
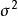
m——測量值。

如果確定了R及，則常態分配曲線就可以確定。現在需要解決的是在已知一組被測量後如何估算R及。

算術平均值和剩餘誤差

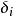首先，在不考慮系統誤差和粗大誤差的條件下，對被測量作多次測量，由於各種隨機因素的影響，即便在同樣條件下，各次測量值均有一定的差異。設測量序列，則用絕對誤差表示的隨機誤差列為

將上式兩邊求和得

或

由常態分配的抵償特性，得

故由式(1)得

式(2)左邊即為隨機變數的數學期望，當n為有限值時，測量值序列的算術平均值為

式中：為測量值序列的算術平均值。

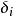
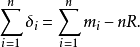
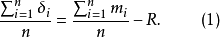
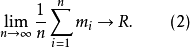
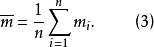
式(2)和式(3)表明，無系統誤差存在時，當測量次數n無限增大時，測量值的算術平均值與真值無限接近。因此可以說，在等精度測量中，算術平均值是被測量最可信賴的值。

由此可見，如果能夠對某一被測量進行無限次測量，就可以得到不受隨機誤差影響的測量結果，或者影響很小，可以忽略不計。但由於實際測量都是有限次測量，處理時只能把算術平均值作為被測量的真值的最佳近似值，於是有剩餘誤差（殘餘誤差）表達式：

式中 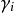為剩餘誤差。

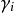
剩餘誤差的性質

剩餘誤差有兩個性質：

剩餘誤差的代數和為零，即

利用剩餘誤差的這一性質，可以檢驗計算的剩餘誤差和算術平均值是否準確。

剩餘誤差的平方和為最小，即

這是最小二乘法原理，在試驗數據處理中常常用到。