基本介紹
- 中文名:箏形
- 外文名:deltoid
- 定義:有一條對角線所在直線為對稱軸
- 性質:軸對稱
- 類型:幾何圖形
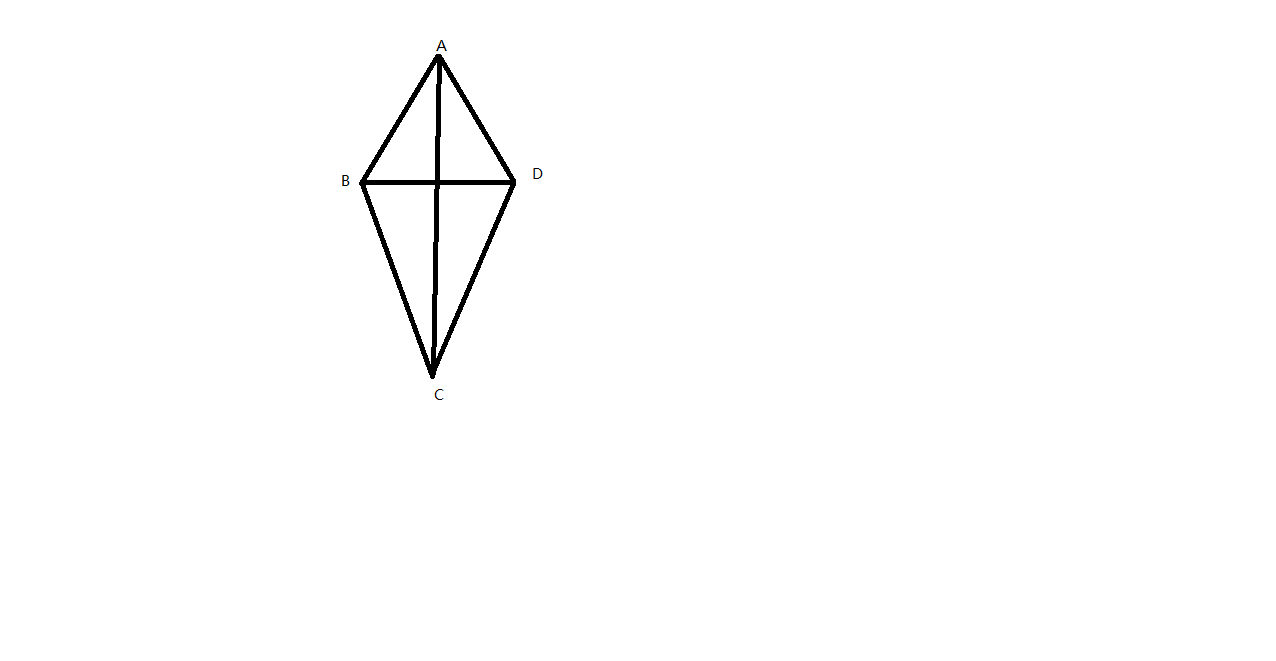
箏形是指有一條對角線所在直線為對稱軸的四邊形,與菱形定義相對應。注意:菱形是特殊的箏形。箏形有內切圓,內切圓圓心是箏形的對稱軸和等角的平分線的交點。...
箏形(kite) 亦稱偏菱形。箏形分凸箏形和凹箏形兩種。特殊的四邊形之一。凹箏形又稱鳶形。...
箏,又稱古箏、秦箏,約(公元前221年-公元前207年)中國古老的傳統彈撥樂器。箏的撥奏在民間廣大地區的流傳中,融合地方民間音樂,形成有不同音樂風格和演奏技法的...
牙箏,是朝鮮族弓拉弦鳴樂器。歷史較為悠久,形制與箏近似,音色圓潤寬厚,可用於合奏或為戲曲伴奏。流行於遼寧、吉林、黑龍江等省,尤以吉林省延邊朝鮮族自治州最為...
《哀箏》的作者是李商隱,被選入《全唐詩》的第540卷第61首。...... 《哀箏》的作者是李商隱,被選入《全唐詩》...箏形似鶴,其奏則如鶴“延頸而鳴”。...
納西箏,納西族彈撥弦鳴樂器。納西語稱扎(Za)。流行於雲南省麗江納西族自治縣。...... 納西箏形狀構造 編輯 形制與漢族箏相同。在納西族的一首民歌《軋砍砍》...
1990年,CMO出現了箏形蝴蝶定理。 [4] 蝴蝶定理定理意義 編輯 蝴蝶定理是古典歐式平面幾何的最精彩的結果之一。這個定理的證法不勝枚舉,至今仍然被數學熱愛者研究...
雙心四邊形是既有內切圓又有外接圓的四邊形。...... (3)延長AO交圓O於C,此時即作出箏形ABCD;(4)作箏形的內切圓I(箏形都有內切圓);(5)擦除箏形;...
鷂形,在台灣稱作鷂形,在中國大陸稱為箏形。是一種四邊形。...... 鷂形,在台灣稱作鷂形,在中國大陸稱為箏形。是一種四邊形。特點為:是圓形的外切四邊形 其中兩...
雙反四角錐(英語:TetragonalAntidipyramid)是一個由四個全等的箏形組成的立體圖形,是八面體的一種。每一個四方偏方面體也是鳶形多面體。其為反四角柱的對偶。....
