等距嵌入問題

等距嵌入問題(isometric imbedding problem)是子流形幾何的一個重要問題。黎曼流形等距地嵌入到高維歐氏空間中作為子流形的問題。它是黎曼幾何學中由來已久的重要問題。

基本介紹

• 中文名：等距嵌入問題
• 外文名：isometric imbedding problem
• 領域：數學
• 學科：子流形幾何
• 人物：雅內特

概念

等距嵌入問題(isometric imbedding problem)是子流形幾何的一個重要問題。黎曼流形等距地嵌入到高維歐氏空間中作為子流形的問題。它是黎曼幾何學中由來已久的重要問題。雅內特(Janet，N.)於1926年，嘉當(Cartan，E.)於1927年，就局部等距嵌入問題，即黎曼流形的一個局部區域等距嵌入到高維歐氏空間的問題，獨立地證明了如下定理：任意n維解析黎曼流形能夠局部等距地嵌入到：

維歐氏空間中。但是，若去掉解析性的要求，問題至今尚未解決。例如，對於最簡單的n=2的情況，至今仍不知道一個高斯曲率變號的二維黎曼流形是否總可以局部等距嵌入到三維歐氏空間中。關於曲面的整體等距浸入問題，有著名的外爾問題：若二維黎曼流形M同胚於球面且高斯曲率恆正，則M能整體等距浸入到R中嗎?這個問題已被尼倫伯格(Nirenberg，L.)和波戈列洛夫(Погорелов，А.В.)先後解決。亞歷山德羅夫(Александров，А.Д.)則用完全不同的所謂凸度量理論的方法解決外爾問題。關於雙曲平面，有著名的希爾伯特定理：常負高斯曲率的完備曲面不能C階等距浸入到R中。後來葉菲莫夫(Ефимов，Н.В.)把上述定理的條件改進為嚴格負高斯曲率的完備曲面。

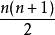
子流形幾何

子流形幾何是微分幾何的一個分支。主要研究黎曼流形中各種子流形的結構及其性質。如極小子流形、常平均曲率子流形等。子流形幾何與微分幾何本身具有同樣悠久的歷史，它們都是在經典三維歐氏空間中的曲線論和曲面論的基礎上發展起來的。在很長一段時期里，子流形幾何學的發展僅限於局部性質的研究。隨著微分流形理論和整體微分幾何學的迅速發展，現代子流形幾何學主要研究黎曼流形中各種子流形的整體性質，尤其是局部性質與整體性質的關係。實和復空間形式中的子流形理論是子流形幾何學的重要方面。子流形幾何學還與數學的其他分支學科密切相關，如微分方程、複變函數論、拓撲學、李群論、數學物理等，並且促進了這些學科的發展.可以說，子流形幾何是微分幾何中歷久不衰的一個分支。

流形

流形是一類特殊的連通、豪斯多夫仿緊的拓撲空間，在此空間每一點的鄰近預先建立了坐標系，使得任何兩個(局部)坐標系間的坐標變換都是連續的。n維流形的概念在18世紀法國數學家拉格朗日的力學研究中已有萌芽。19世紀中葉英國數學家凱萊(1843)、德國數學家格拉斯曼(1844，1861)、瑞士數學家施勒夫利(1852)分別論述了n維歐幾里得空間理論，把它視為n個實變數的連續統。1854年德國數學家黎曼在研究微分幾何時用歸納構造法給出一般n維流形的概念：n維流形是把無限多個(n-1)維流形按照一維流形方式放在一起而形成的，從此開始流形的拓撲結構及其局部理論的研究。法國數學家龐加萊在19世紀末把n維流形定義為一種連通的拓撲空間，其中每一點都具有和n維歐氏空間同胚的鄰域(被稱為龐加萊流形)，從而開闢了組合拓撲學的道路。

對流形的深入研究集中在流形上的微分結構與組合結構的存在性、唯一性問題，微分結構與組合結構的關係，流形的各種意義下的分類等問題，20世紀50—60年代做出許多重要結果，近幾十年來出現有限維帶邊流形和無限維流形概念。流形理論在與其他拓撲理論的相互結合發展中也提出許多問題，其研究仍在繼續。

黎曼流形

黎曼流形是一黎曼度量的微分流形。設M是n維光滑流形，若在M上給定一個光滑的二階協變張量場g，稱(M，g)為一個n維黎曼流形，g稱為該黎曼流形的基本張量或黎曼度量，如果滿足：

1.g是對稱的，即：

g(X，Y)=g(Y，X) (X，Y∈T_pM，p∈M).

2.g是正定的，即：

g(X，X)≥0 (X∈T_pM，p∈M)，

且等號僅在X=0時成立。

簡單地說，黎曼流形就是給定了一個光滑的對稱、正定的二階張量場的光滑流形。

在微分流形以及黎曼幾何中，一個黎曼流形是具有黎曼度量的微分流形，換句話說，這個流形上配備有一個對稱正定的二階協變張量場，亦即在每一點的切空間上配備一個正定二次型。給了度量以後，我們就可以像初等幾何學中一樣，測量長度，面積，體積等量。