一種把球面直角坐標系即經緯網通過投影轉繪而成的平面網。在這平面網上不同位置的單位面積都相等。W.施密特於1925年把這種投影網用於構造地質學，又稱施密特網。
基本介紹
- 中文名：等積投影網
- 外文名：equal-area net
- 別稱：施密特網
- 學科：地理信息系統
- 出現時間：1925年
- 提出人：W.施密特
等積投影,製圖原理,
等積投影
等積投影(equal-area projection)是地圖投影的一種（圖1），是地圖上任何圖形面積經主比例尺放大以後與實地上相應圖形面積保持大小不變的一類投影。即投影面積與實地面積相等的投影——面積比為1。滿足等積條件，在地圖投影中最容易達到。
地圖上任一圖形面積與實地上相應的面積相等。即面積變形等於零。為了保持等積條件，需使面積比等於1。常見的等積條件形式有：①P= mnsinθ=1(P為面積比，m為經線長度比，n為緯線長度比，θ為經緯線投影后的夾角)；②P=ab=1(a為某點上最大長度比，b為某點上最小長度比)。在等積投影的不同點上，由於最大長度比不斷增大，最小長度比不斷縮小，因而形狀變化比較大，角度變形也比較大。由於這類投影沒有面積變形，故有利於在地圖上進行面積對比。
變形橢圓為長短軸各不相同的橢圓，面積相等，但角度變形最大，主要是依靠增大角度變形而保持面積相等。用這種投影編制的地圖，因為面積沒有變化，所以有利於在地圖上進行面積對比，但形狀變形比其他投影大。多用來繪製經濟圖，行政區圖和人口圖。
圖1
圖1製圖原理
設T為半徑為R的球面上的一點，透視投影平面與之相切於通過T的直徑的另一端點T',則球心角θ的P點的T'P聯線成為投影平面上的線段T'P'(圖2)，即
，則由此所製得的投影網──施密特網的外圓半徑為r，而r與R的關係為
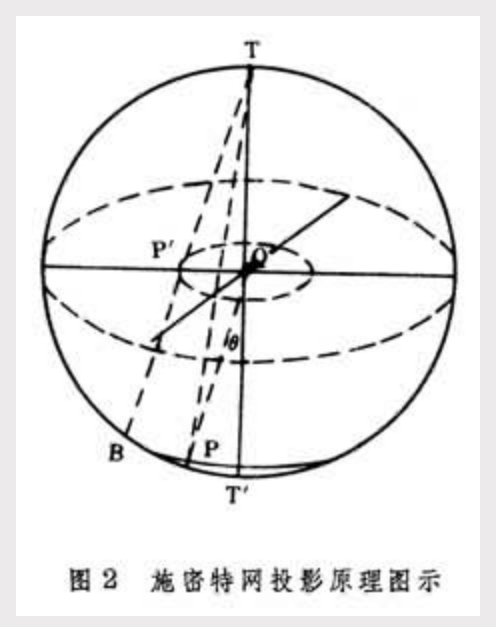
從而使施密特網內不同位置的單位面積保持相等。由於沒有保角性，球面小圓除圓心與網心重合的圓仍為圓外，其他位置上的圓在施密特網內為四級橢圓或橢圓弧，施密特網的經、緯線也都是四級橢圓弧線。這種橢圓短徑與施密特網的徑向一致。
