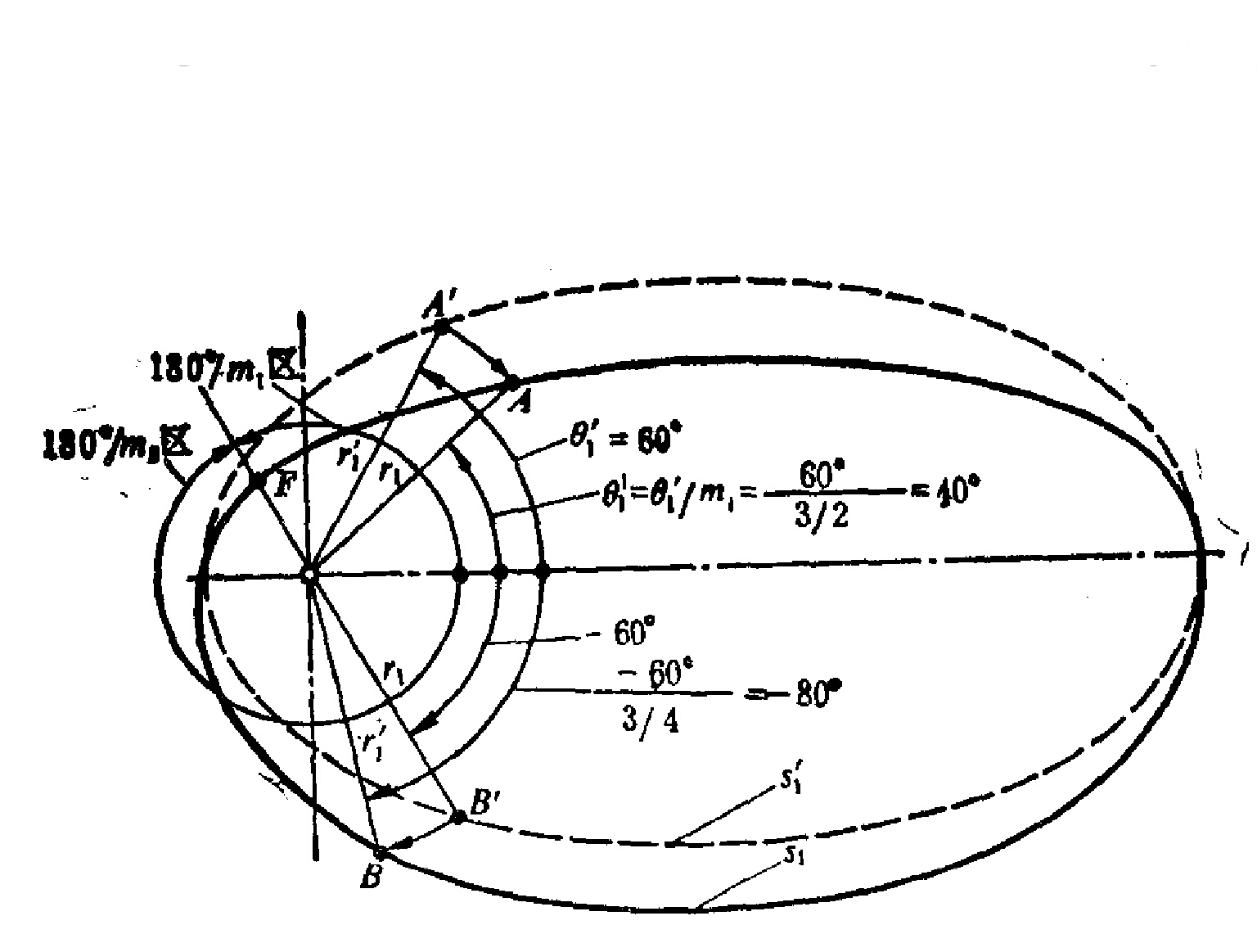
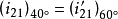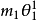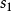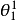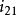變形橢圓指為顯示變形的幾何圖形。這是用來概括和直觀地表達變形特徵的幾何圖形。假設考慮地面(地球橢球體面)是一個微小的無窮小圓(稱微分圓),在投影中發生變形後,往往不能保持為圓形,而是一個橢圓,稱為變形橢圓。
基本介紹
- 中文名:變形橢圓
- 外文名:ellipse of deformation
- 含義:指為顯示變形的幾何圖形
- 來源:投影
- 特點:形狀變化很大,但面積大小相等
- 套用學科:數學術語
概念,基本原理,
概念
假設考慮地面(地球橢球體面)是一個微小的無窮小圓(稱微分圓),在投影中發生變形後,往往不能保持為圓形,而是一個橢圓,稱為變形橢圓。根據變形橢圓的形狀和大小,能反映出投影中變形的質和量的差別,同時具有直觀的明晰形。如在等角投影中,變形橢圓保持正圓形,但在不同的位置上,面積差異很大,而在等積投影中,則變形橢圓形狀變化很大,但面積大小相等。
基本原理
兩個全等橢圓相滾動,如圖1中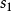 、
、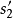 及圖2中
及圖2中 、
、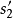 ,其傳動比
,其傳動比 作對稱變化,如圖3中
作對稱變化,如圖3中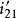 ;而兩個變形橢圓相滾動,如圖2中的
;而兩個變形橢圓相滾動,如圖2中的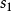 、
、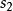 ,傳動比則可作不對稱變化,如圖3中的
,傳動比則可作不對稱變化,如圖3中的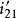 。
。
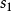
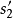

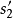

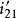
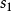
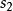
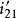
 圖1
圖1 圖2
圖2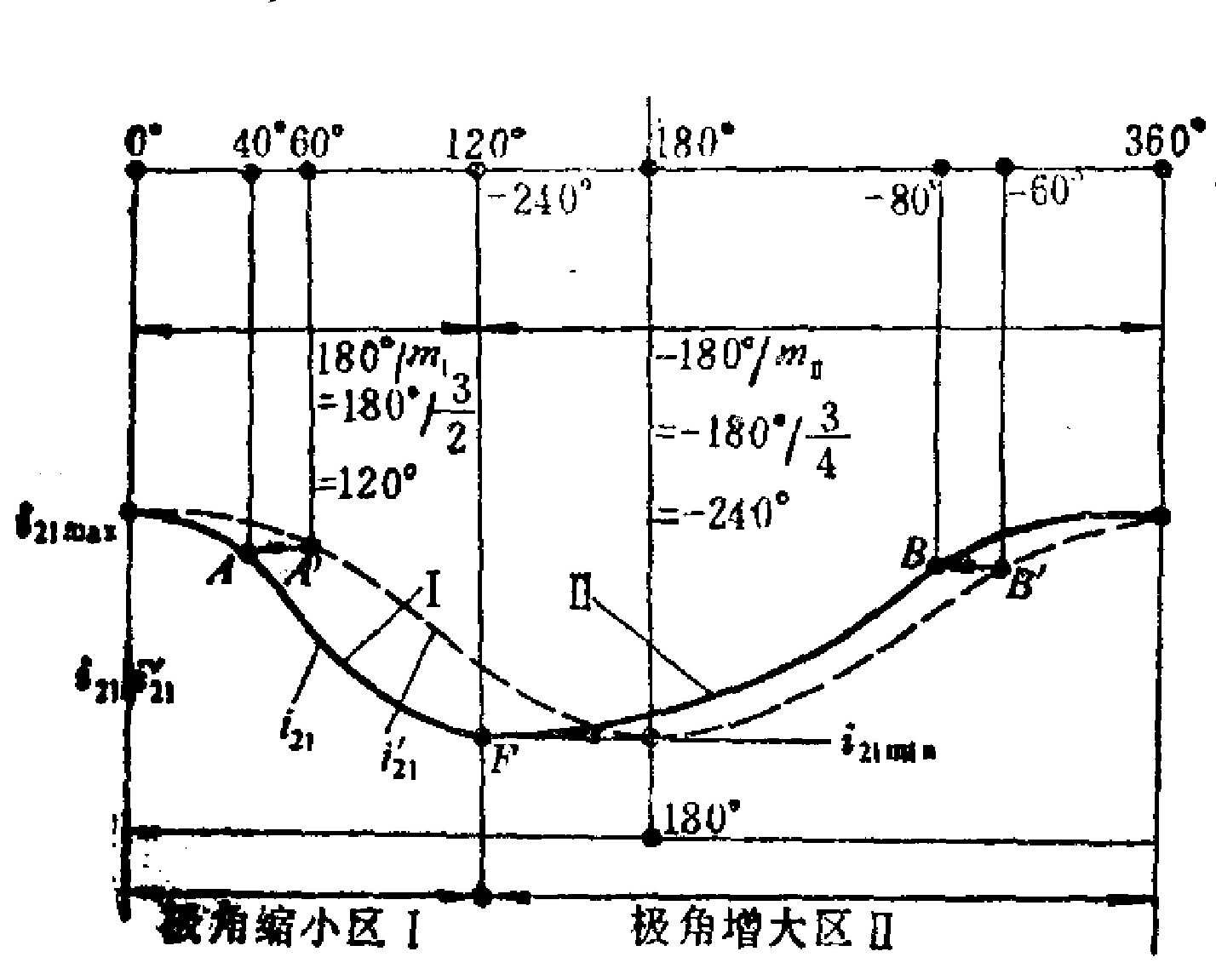 圖3
圖3圖2表示如何由原始橢圓 導出稱為變形橢圓的
導出稱為變形橢圓的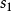 。圖中兩橢圓極徑
。圖中兩橢圓極徑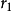 相同而極角
相同而極角 則不同。在極角縮小區內,極角縮小係數
則不同。在極角縮小區內,極角縮小係數 ,縮小區域占
,縮小區域占 ,例如圖2中
,例如圖2中 上點
上點 處極角
處極角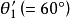 縮小成
縮小成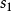 上點
上點 的極角
的極角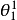
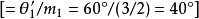 ,但點
,但點 、
、 處的極徑
處的極徑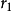 不變,這樣
不變,這樣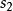 、
、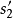 相應的極徑
相應的極徑 不變,圖3中的
不變,圖3中的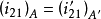 亦不變。在極角增大區內,極角增大係數
亦不變。在極角增大區內,極角增大係數 ,增大區域占
,增大區域占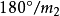 ,例如圖2中的
,例如圖2中的 上點
上點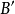 的極角
的極角 (“
(“ ”號僅表反向量度)增大為
”號僅表反向量度)增大為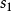 上點
上點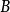 的極角
的極角 ,但點
,但點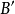 、
、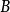 處的極徑
處的極徑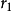 不變,這樣
不變,這樣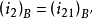 亦不變(見圖3)。變形橢圓
亦不變(見圖3)。變形橢圓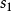 (圖2)及其不對稱的傳動比
(圖2)及其不對稱的傳動比 (圖3)就是基於這種方法由原始橢圓
(圖3)就是基於這種方法由原始橢圓 推導出來的。上述
推導出來的。上述 、
、 要滿足
要滿足

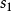
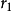





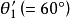
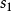

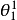
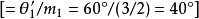


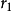
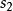
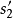

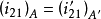

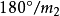

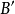


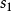
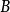

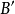
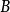
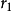
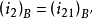
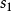





從圖3可知,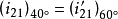 ,所以只要將用於原始橢圓
,所以只要將用於原始橢圓 中的
中的 用
用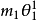 代入即得變形橢圓
代入即得變形橢圓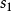 在
在 區
區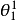 處的傳動比
處的傳動比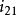 。
。